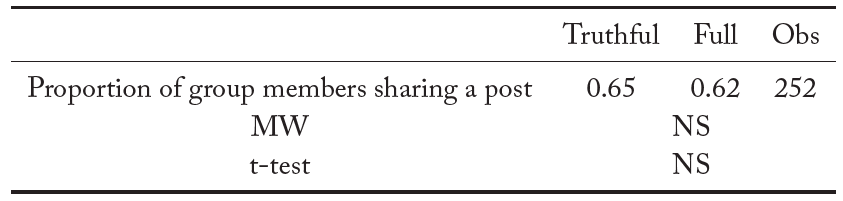1 Introduction
Information held by voters is crucial in determining policy choices. Social media platforms play an increasingly pivotal role in determining the information available to voters.1Social media sites have surpassed print newspapers as a news source for Americans: One in five U.S. adults say they often get news via social media, slightly higher than the share who often do so from print newspapers (16%) for the first time since Pew Research Center began asking these questions (https://www.pewresearch.org/fact-tank/2018/12/10/social-media-outpaces-print-newspapers-in-the-u-s-as-a-news-source/) Voters are exposed to information via social media, and can themselves provide information to others. By increasing the availability of information to voters, social media has the potential to increase informedness. However, partisan preferences among social media users may lead to perverse outcomes. 2Empirically it has been noted by Boxell et al. (2018) that partisanship pre-dates the advent of social media platforms. First, users may strategically withhold information that does not support their preferences, thus potentially distorting beliefs.3Garz et al. (2020) find that individuals are more likely to interact with posts that conform to their partisan bias on Facebook. In a sender-receiver game, individuals are more likely to withhold unfavorable information Jin et al. (2015). Second, users may post false information to affect voter beliefs and policy outcomes. Recently, there has been a lot of attention paid to the latter, particularly related to elections.
Does social media increase the quality of voting outcomes and voter welfare, both when it is and is not possible to use the platform to disseminate misinformation? In this paper, we study how voters acquire and share information in the presence of partisanship in a laboratory experiment. We consider three information sharing protocols. In the first, there is no social media platform, and information sharing is thus not possible. Second, we allow voters to accurately share the information they purchase via the social media platform (truthful information sharing protocol). Third, voters are additionally permitted to post misinformation on the social media platform (full information sharing protocol).
To effectively address the effect of misinformation, it is important that our laboratory environment reflect several important features of reality, while simultaneously allowing us to directly measure outcomes that more typically unobservable in naturally occurring data. These features include the ability of individual voters to acquire costly information themselves, to share and gather information on a social media platform with an endogenous network structure where the information on social media can be inaccurate. In order to measure the effect of partisan preferences on the part of voters, as opposed relying on unobserved variation in homegrown preferences, it is also important to induce voter bias.
In our setup, there is an unknown and binary state of the world. Each voter receives a fixed payoff if the voting outcome matches the underlying state. However, each voter also receives a partisan payoff that only depends on the voting outcome, and is independent of the state of the world. These partisan preferences vary continuously from moderate to extreme. Each voter has the option to purchase information about the underlying state before voting. When social media is present, before votes are cast, voters choose which group members to follow. They then can share a post about the information they purchased. Voters can only see the posts of group members they are following.
In the absence of social media, our environment is similar to that of Martinelli (2006), which provides a theoretical benchmark of information acquisition without communication. When communication via a social media platform is introduced, theoretical analysis is intractable. As such, our experiment exploratory, as discussed in (Smith, 1982). In short, we have purposefully chosen an environment that reflect critical aspects of reality, so that the resulting data can inform policy debates surrounding misinformation, rather than focusing on a tractable model. This experiment is a first step towards using the lab as a test-bed for effectively combating misinformation.
We find that introducing a social media platform increases the quality of group decision making when messages are restricted to be truthful.4Quality of group decision making is defined as the share of observations where the group’s vote matched the state of the world. However, allowing misinformation on the platform erases these gains. In fact, both welfare and the quality of group decision making is lowest when it is possible to share misinformation.5Total welfare is defined as the sum of all the earnings of group members.
With the introduction of a social media platform, group members across the partisan spectrum purchase more units of information. Therefore, the lower quality of decision making in the presence of misinformation is not driven by voters being less individually informed. Misinformation results in voter’s expending more resources on information, but not improving the quality of decision making.
In the truthful information sharing protocol, group members share over 90% of the information purchased. In contrast, when misinformation is possible, only 50% of the information purchased is shared accurately on the social media platform. Further, we observe fewer connections on the social media platform when misinformation is permissible. In fact, the relatively low level of connections when misinformation is possible is the primary channel that explains the lower quality of decision making even after we account for the total information purchased by all group members. This result is of particular importance, as it demonstrates that social media platforms may have a vested interest in policing misinformation.
Specifically, user engagement, as measured by the number of people a user follows, is reduced by misinformation. While Mark Zuckerberg has stated, “I don’t think that Facebook or internet platforms in general should be arbiters of truth,” our results suggest that it may be in Facebook’s interest to police misinformation.6https://www.cnbc.com/2020/05/28/zuckerberg-facebook-twitter-should-not-fact-check-political-speech.html.
This paper contributes to two strands of the literature studying voting behavior: endogenous information acquisition and communication. To the best of our knowledge, we are the first to study costly information purchase and communication in the presence of continuous partisans within a group. So far, literature studying information acquisition decisions have considered homogeneous groups (Elbittar et al., 2016, Grosser and Seebauer, 2016, Bhattacharya et al., 2017). Goeree and Yariv (2011), Pogorelskiy and Shum (2019), Le Quement and Marcin (2019) only consider a limited number of discrete partisan types in a group. Introducing continuous partisans allows us to study how the degree of partisanship influences the quality of information shared on the social media platform. Goeree and Yariv (2011), Le Quement and Marcin (2019) report largely truthful revelation of information on the group message board. In contrast, we find that 47 percent of posts shared on the social media platform contain misinformation. We find a positive correlation between the likelihood of sharing misinformation and the degree of partisanship.
Both the literature studying information acquisition (Elbittar et al., 2016, Grosser and Seebauer, 2016, Bhattacharya et al., 2017), and that on communication (Goeree and Yariv, 2011, Pogorelskiy and Shum, 2019, Le Quement and Marcin, 2019) only consider homogeneous quality of signals if an individual receives a signal. We extend the literature by allowing for heterogeneity in the signal’s quality within a group. In our experiment, individuals choose the accuracy of the signal they purchase.7Individuals can purchase 1–9 “units” of information; each “unit” of information increases the accuracy by 5 percent. This allows us to study information aggregation and communication in a more robust setting.
Second, to the best of our knowledge, we are the first to study information aggregation on an endogenous social media platform. Pogorelskiy and Shum (2019) imposes three social networks–null, complete, and partisans, where individuals can share information truthfully. We find that even with partisan preferences, groups primarily form complete networks.8On average individuals have 3.75 connections in the truthful information sharing protocol, and 3.35 connections in the full information sharing protocol.
1.1 Literature overview
The paper studies three strands of the literature: partisanship, communication, and endogenous information acquisition, in a cohesive framework.
Battaglini et al. (2010), in their seminal paper, study the swing voter curse in a controlled laboratory setting. In the absence of partisan voters, uninformed voters strategically abstain from voting.9Uninformed independent voters would abstain from voting and so delegate the responsibility to more informed voters (Feddersen and Pesendorfer, 1996). In the presence of strict partisan preferences for one of the two options, in larger groups, a higher share of uninformed voters vote to counteract partisans’ effect in the group, as predicted by theory.
Guarnaschelli et al. (2000) study voting behavior in the presence of communication via straw polls with groups with a common interest. Communication improves information aggregation across both the voting rules. Goeree and Yariv (2011) extends the framework in Guarnaschelli et al. (2000) to allow for unrestricted communication and heterogeneity in group composition: weak and strong partisans across three voting rules. They find that individuals accurately reveal private information in both the weak partisan and strong partisan treatment, which leads to better information aggregation and improved quality of group decision making. Le Quement and Marcin (2019) observes a similar pattern of truthful sharing of private signals with restricted communication in a three-person group even when the partisan bias is disclosed along with the straw vote results.10Groups communicate using straw votes.
Pogorelskiy and Shum (2019) study the role of media bias on the quality of group decision making in the presence of weak partisans in a group. Group members have an option to share their signals truthfully on a social media platform. They vary two fixed social network structures and the degree of bias in the media signals. They find that communication through the social network improves the quality of decision making relative to no social media. However, biased media signals lower the quality of group decisions.
Elbittar et al. (2016) study heterogeneity in the cost of acquiring information across majority and unanimity decision rules. They find low levels of information purchase and frequent voting by uninformed voters even when they have a choice to abstain from voting, which lowers the quality of group decisions significantly. Grosser and Seebauer (2016) focus on the majority rule and compare voluntary and mandatory voting; similar to Elbittar et al. (2016) they report under-purchase of information and a penchant for uninformed voting. Bhattacharya et al. (2017) points out that the signal’s precision is an essential determinant of information acquisition. When signals are perfect, i.e., revealing the state of the world with certainty, theory predicts the data well. However, groups tend to over-purchase signals compared to the equilibrium prediction.
2 Theory
We study an election with two alternatives, A and B. There are voters (
). A voter’s utility depends on the chosen alternative
, the state
, and the quality of information acquired by the voter
. Acquiring information of precision
has a cost given by
.
Voters have heterogeneous preferences: we assume that for each for ,
, where
is drawn from an uniform distribution over
. The remaining of the preference parameter is
,
and
. The random variable is drawn independently for each voter. 11We build on the model with heterogeneous preferences in \cite{martinelli2006would}, where a voter preference is given by
, and
. The utility for vote
can be written as
. We assume that the cost function is convex, twice differentiable, and
.
At the start of the round, nature selects a state. The prior probability of state is
, and the prior probability of state
is
. In our set up we assume
. Each voter decides the quality of information they’ll acquire,
, after learning about the value of
. Each voter receives a signal
depending on the value of
selected. The probability of receiving signal
in state
is equal to the probability of receiving signal
in state
and is given by
. The likelihood of getting the correct signal is increasing in
. If
the signal is uninformative. Signals are private information. Voting takes place after everyone receives their signals. A voter can vote for either A or B. The alternative which receives the majority of the votes is chosen.
An action in this model is a triple , where
specifies the quality of information,
specifies which alternative to vote for after receiving the signal
, and
specifies which alternative to vote for after receiving signal
. A strategy for voter
is now a mapping:
which specifies the action for every realization of the preference parameter .
Based on (Martinelli, 2006, Theorem 5) we find the strategies for realizations of .
Theorem 1. In the model with heterogeneous preferences, if , there is an equilibrium with information acquisition, and it is unique within the class of equilibria with information acquisition. The equilibrium mapping is
(1)
Proof in Appendix 5
In the experiment we use the following parameters ,
,
, and
, where
. For these parameters we solve for equilibrium values of
and
based on results from Theorem 1:
(2)
2.1 Social media platform
We allow for endogenous network formation on the social media platform. Voters choose which group members they want to follow on the social media platform. A voter can only see information shared by members they are following. The group members do not get to see information shared by their followers if they do not choose to follow them on the platform. Voters learn which group members are following them, and simultaneously decide whether they want to share a post. A post contains the following information: value of ui, (ii) x, and (iii) We study the following three information sharing protocols.
-
- No information sharing: This is the default setting in Martinelli (2006), where a voter casts their vote directly after purchasing information.
- Truthful information sharing: If a voter chooses to share a post, the result from their information purchase decision is shared as a post on the group message A voter still has a choice whether to reveal ui.
- Full information sharing: If a voter chooses to share a post, the voter chooses the content of their There is a possibility of misrepresenting the information.
The effect of social media platforms on the level of information acquisition, and the likelihood that groups are able to vote for the underlying state of the world, is an open empirical question. While this question is of tremendous practical importance, modeling the equilibrium effects is not tractable. Rather than proceed under restrictive assumptions which render the model uninteresting, we turn to laboratory experiments to provide guidance. Our goal in doing so is to be able to study behavior in games that are quite close to reality. This allows us to offer insights that have clear policy implications, while also offering insights that can aid in the formulation of new theories.
The quality of group decision making is likely to depend on the amount of information purchased and aggregated by the group. In the absence of social media, equilibrium behavior involves some voter types buying information and voting in line with their signal, while other types remain uninformed and vote according to their partisan preferences. Thus, the only avenue for information aggregation is via the voting process.
A social media platform affords the group an additional avenue: any signal that is shared can affect the beliefs, and thus the votes, of any group member who sees it. However, if group members strategically withhold information from the social media platform, information sharing can distort beliefs and voting patterns. Further, when it is possible to share misinformation, information aggregation is difficult, as it is unclear whether posted information is false, selectively revealed, or both.
Since information sharing on social media may have perverse effects, the amount of information purchased by individuals may be affected, and this effect may depend on the potential presence of misinformation. Further, misinformation may affect the density of a social network, the propensity of individuals to make posts, the content of any posts, and individual voting decisions.
3 Experiment Procedure and Design
A session consists of two stages of several rounds each. In every stage, groups play five rounds with certainty, and there is a 90% continuation probability for each additional round.12The number of rounds is pre-randomized for all groups. Groups interact in 18 rounds in the first stage, and 24 rounds in the second stage. Subjects are not aware of the number of rounds in each stage. At the start of each stage, subjects are randomly matched to form groups of five, and each subject is randomly assigned a subject ID (A, B, C, D, or E). The group composition and subject ID are fixed within a stage.
At the start of each stage, each subject observes their type. Each subject’s type, p, is an i.i.d. draw from a discrete uniform distribution with support {0, 1, . . . , 99, 100}, and this is common knowledge. Subject types are private information and are constant throughout a stage. There are two possible states of the world in each round, Brown or Purple, and each is equally likely.
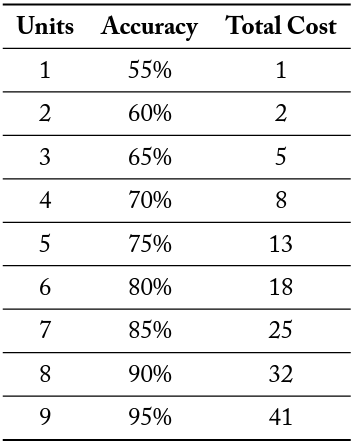
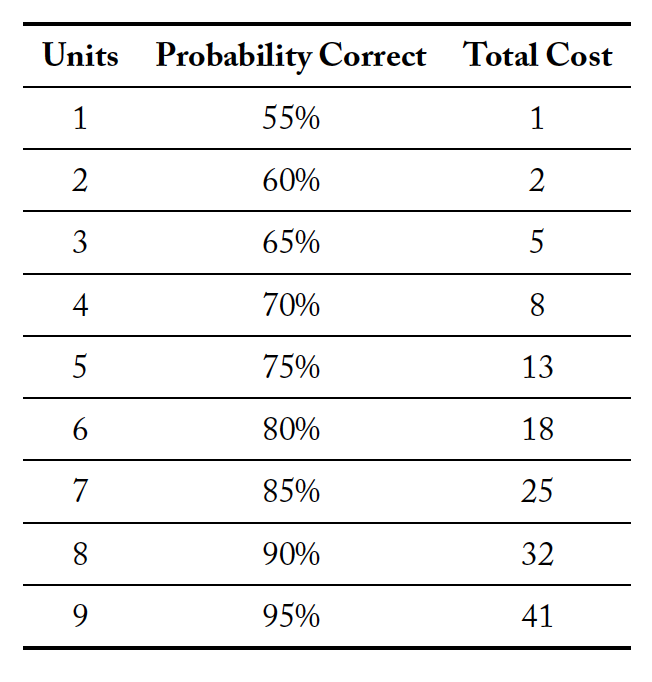
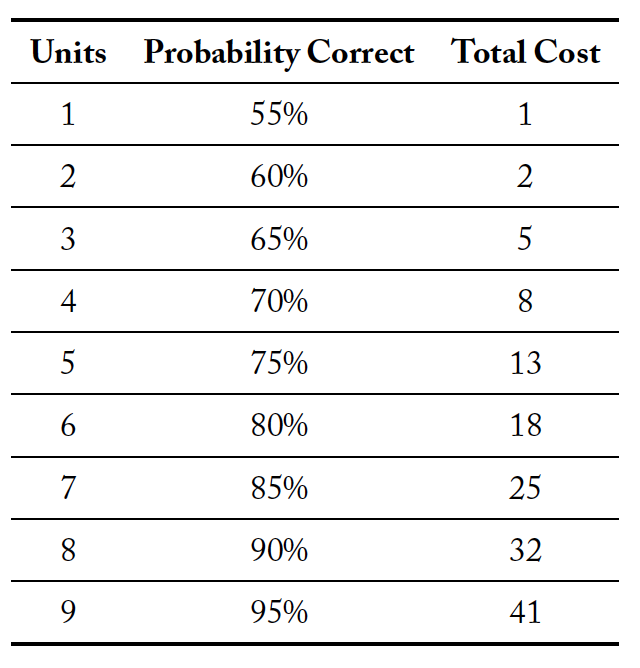
While subjects do not directly observe the state of the world, they can purchase a binary signal. The probability with which this signal corresponds to the underlying state depends on how many “units” of information the subject purchases. Specifically, if a subject purchases one unit of information, the signal is accurate 55% of the time. Each additional unit purchased increases the accuracy of the signal by 5%.
Crucially, the marginal cost of these units is increasing. Table 1 specifies the cost function of units of information as it was presented to subjects. If a subject decides not to buy information, they do not receive a signal. Each signal is conditionally independent.
Table 1. Cost of Information
After making their purchase decisions, subjects may be able to communicate with other group members via a social media platform. On this platform, subjects first choose whether to “follow” other members of their group and then decide whether to make a post. Following another subject allows one to see the post of the corresponding subject in that round, provided they decide to make a post. In the first round of a stage, each subject follows all group members by default and could unfollow any or all of them before posts are made. In each subsequent round, a subject can revise whom they follow. After everyone makes their connection decisions, subjects learn which group members are following them, and decide whether they want to share a post. A post contains up to three components.
- A number of units of
- A signal: Brown, Purple, or
- A Revealing a type is optional.
After each subject views any posts made by those group members they follow, if any, subjects simultaneously vote for either Brown or Purple. The color which gets three or more votes is the group’s decision. The payoff corresponding to the voting outcome has two parts. The first depends on p. A subject i gets a payoff of pi EF if the group’s decision is Brown and 100 − pi EF if the majority votes for Purple.13Subjects’ earnings are denominated in Experimental Francs (EF ) which are converted back to USD at 145EF = $1. Note that this is independent of the state of the world. We refer to this as their partisan payoff. The second part depends on the state of the world. If the group’s decision matches the randomly assigned state of the world, each subject gets a payoff of 50 EF. The final payoff for the round is the payoff from voting minus the cost of buying information. At the end of the round, subjects also receive feedback about the randomly assigned state of the world and the color the group voted for.
We consider three information-sharing protocols.
- No information sharing: after individuals purchase information, they cast their votes, and have no opportunity to share information.
- Truthful information sharing: the contents of the post are pre-populated with the number of units of information they purchased, as well as their realized Subjects still have the option of whether or not to share their type. They may also decline to share a post at all.
- Full information sharing: the subject determines the contents of their post: the number of units of information they purchased, their realized signal, and their type (optional). They may also decline to share a post at all.
We vary the information sharing protocols within subjects. In a given session there were two information sharing protocols. Across the six sessions, we include all possible combinations and orders of these protocols. This allows us to control for order effects, as well as to have clean comparisons between each information sharing protocol. Table 2 illustrates this experimental design.
Table 2. Experiment Design
The experiment was conducted at the ExCEN laboratory at Georgia State University between February and March 2020. A total of 90 subjects participated in the experiment across six sessions of 15 subjects each. The subjects were recruited using an automated system that randomly invited participants via emails from a pool of more than 2,400 students who signed up for participation in economic experiments at Georgia State University. Subjects before entering the laboratory signed an informed consent form. Each session was computerized using z-Tree (Fischbacher, 2007). Subjects were not allowed to communicate with each other.14To ensure privacy, each computer terminal in the lab is enclosed with dividers.
At the start of each stage, subjects were provided with a physical copy of the instructions, which were then read aloud by the experimenter.15See Appendix 5 for a sample set of instructions. After the instructions were read, each subject individually answered a series of quiz questions to ensure comprehension of the game. Each session lasted for approximately two hours and forty-five minutes. The average payoff was $28.5, with a range between $17.5 and $38.
4 Results
4.1 Quality of group decision making
We define the quality of group decision making as the frequency with which the group matches the state of the world. For some realizations of voter types, this outcome does not correspond to the welfare maximizing outcome. However, ex ante, matching the state of the world is optimal from the group’s perspective.
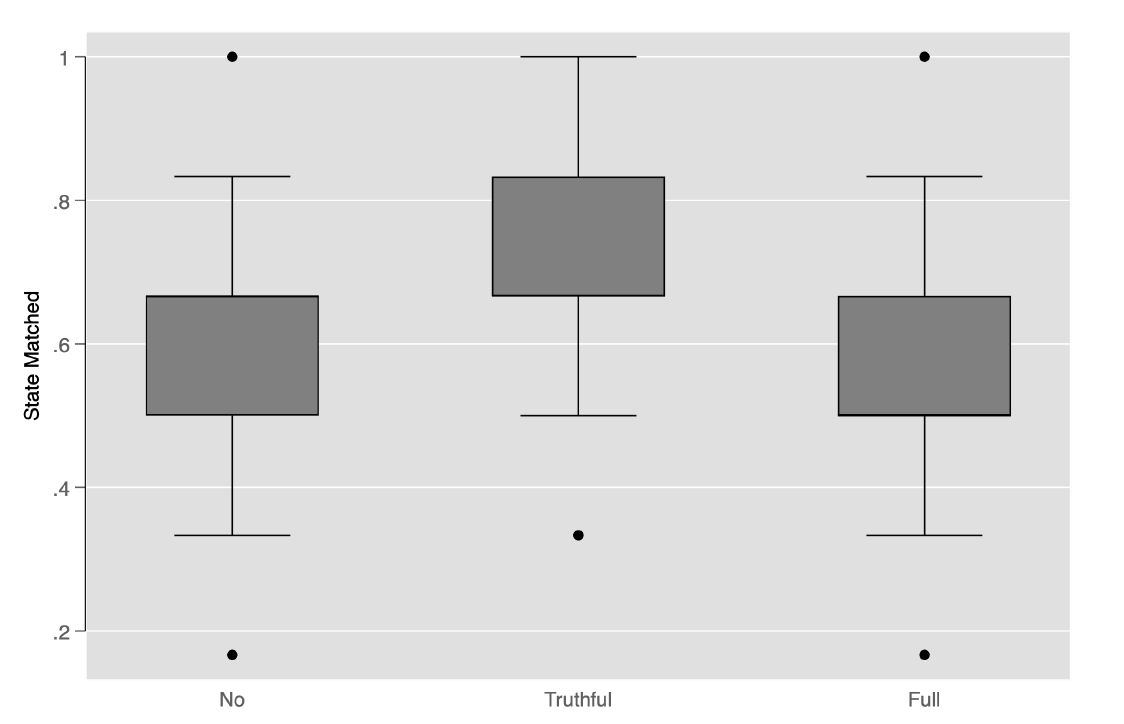
Figure 1 contains boxplots of the quality of group decisions across the three information sharing protocols. Note that social media improves group decision making when it is not possible to share misinformation (Mann–Whitney, p < 0.001).16Throughout our analysis, we report p-values of two-tailed tests. See Appendix 5 for tables containing all relevant parametric and non-parametric tests. However, when misinformation is possible, social media slightly reduces the quality of group decision making, although these differences are not statistically significant (Mann–Whitney, n.s.).17When a test is not statistically significant at conventional levels, we denote this as n.S..
Not surprisingly, when conditioning on the presence of social media, misinformation reduces the quality of group decision making (Mann–Whitney, p < 0.05).
Figure 1. Boxplots of the quality of group decision making by treatment
These results demonstrate that social media has the potential to yield improvements in voting outcomes, provided misinformation can be effectively policed. This is despite the fact that, when misinformation is not possible, partisans on social media have an incentive to reveal information selectively.
4.2 Units of information purchased
Social media can provide users with access to additional information, although the reliability of this information is questionable. Since users are always able to disregard any or all content, one might expect that individual information acquisition would not increase in response to social media. Further, since voter types are uniformly distributed, one would expect that any bias found in social media would be driven by the extreme types on both tails of the distribution. Ex ante, these biases would balance each other, so that social media content is, on average, informative.
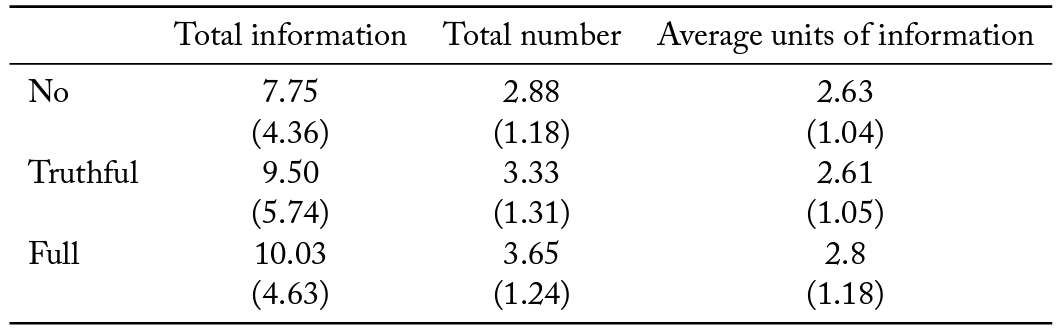
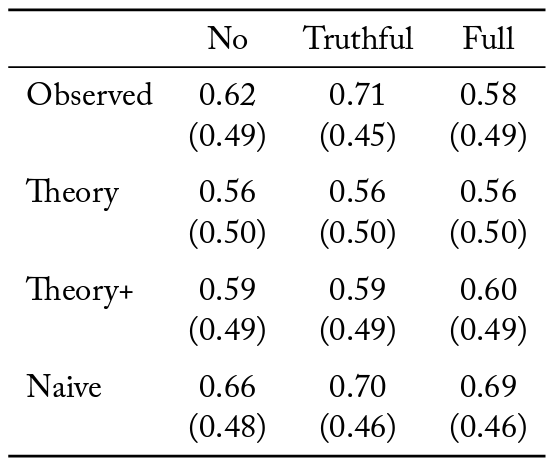
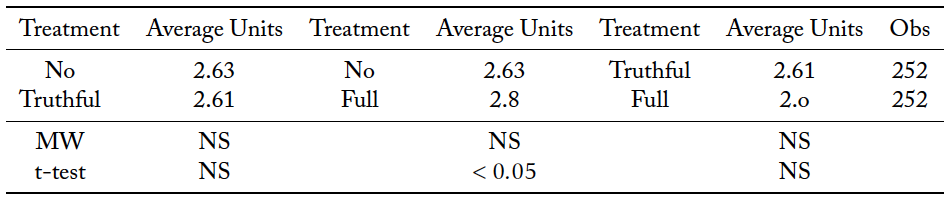
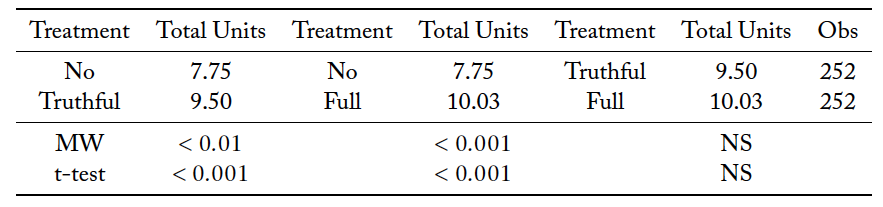
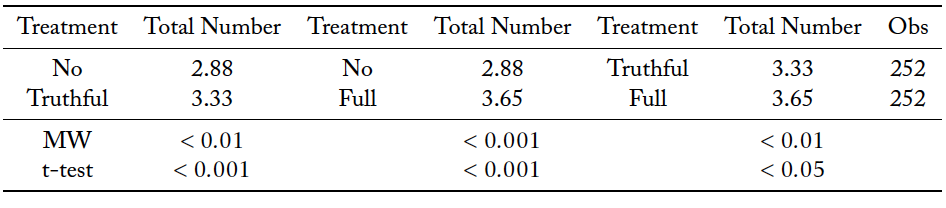
Table 3 shows that the total units of information purchased within a group increase when social media is present. This is true both when misinformation is permissible (Mann–Whitney, p < 0.001), and when it is not (Mann–Whitney, p < 0.001). Interestingly, misinformation does not increase information acquisition when social media is present (Mann–Whitney, n.s.).
There are no statistically significant differences across the three information sharing protocols in the average units of information purchased by a group member (Mann–Whitney, n.s.).
The total information purchased is driven by an increase in the total number of group members acquiring information. Introducing social media increases the number of purchases both when misinformation is present (Mann–Whitney, p < 0.001), and when it is not (Mann–Whitney, p < 0.01). Interestingly, allowing misinformation on social media increases the number of people in the group acquiring information (Mann–Whitney, p < 0.01).
Table 3. Summary statistics of information acquisition decisions by information sharing protocol
Notes: Table contains means with standard deviations in parentheses.
4.2.1 Simulation exercise
Social media increases individual information acquisition, both with and without misinformation. Are voters effectively using this information? Does social media yield gains in the quality of group decision making beyond what could be obtained in its absence, taking the level of observed information acquisition as given?
To address this question, we compare observed group outcomes against three benchmarks under the assumption that voters will only account for information they personally purchased. These benchmarks simulate behavior in the absence of social media.
- Theory: This benchmark is simply the theoretical predictions for the no communication treatment. Individuals p ≤ 36 do not buy information and always vote for Purple, and p ≥ 64 do not buy information and always vote for The individuals in the interior buy two units of information and vote with the color of the signal they received.
- Theory+: This benchmark is similar to Theory, but individuals in the interior vote sincerely based on the number of units of information they actually purchased in the experiment. Individuals in the interior who did not purchase information vote with their partisan preferences, i.e., p < 50 vote for Purple and p > 50 vote for Brown.
- Naive: Individuals who purchase information vote sincerely based on their signal, and individuals who did not purchase information vote for their partisan preference. Note that this benchmark assumes that partisanship does not affect voting behavior for any informed voter, while the uninformed vote according to the partisan Thus, this benchmark simulates outcomes if there is no waste of information.
The results from the simulations are reported in Table 4. In the baseline treatment, the observed quality of group decision making is not statistically different from any of the three theoretical benchmarks, suggesting groups successfully aggregate information purchased by all individuals (median test, n.s.). That is, in the absence of social media, group outcomes are not statistically different from what we would expect if all informed bidders voted based on their signals. This is surprising, as the Naive benchmark strips some of the effects of partisanship out of the problem.
Groups in the truthful information sharing protocol use the social media platform to effectively aggregate information, beyond what is predicted by both Theory (Mann-Whitney, p < 0.001) and Theory+ (Mann-Whitney, p < 0.05). This indicates that the increase in the quality of group decision making relative to the baseline treatment is not entirely attributable to the increase in individual information acquisition. Further, the quality of group decision making is not statistically different from the Naive benchmark (Mann-Whitney, n.s.). This implies that the additional information voters gain via social media improves the quality of group decision making such that it is as if all informed voters simply voted sincerely. Strategic withholding of information on social media is not sufficient to erase the gains made available by the increase in information acquisition, which is caused by introducing social media.
Once misinformation is permitted, the observed quality of group decision making is comparable to Theory and Theory+ (Mann-Whitney, n.s.), but significantly lower than the Naive benchmark (Mann-Whitney, p < 0.05). This suggests that the presence of the social media platform leads to a loss in information aggregation. That is, when misinformation is possible on social media, there are no realized gains in the quality of group decision making, despite the platform inducing additional information purchases. As we will discuss in more detail below, the fact that information is costly means that social media reduces welfare when misinformation is possible.
This exercise demonstrates that social media can lead to an increase in effective information aggregation, provided misinformation is curtailed. That is, voters are able to use information observed on the social media platform to, on average, vote for the outcome corresponding to the true state of the world. This is despite the fact that extreme partisans may have an incentive to strategically withhold information.
Table 4. Quality of decision (simulation)
Notes: Table contains means with standard deviations in parentheses.
4.2.2 Social media
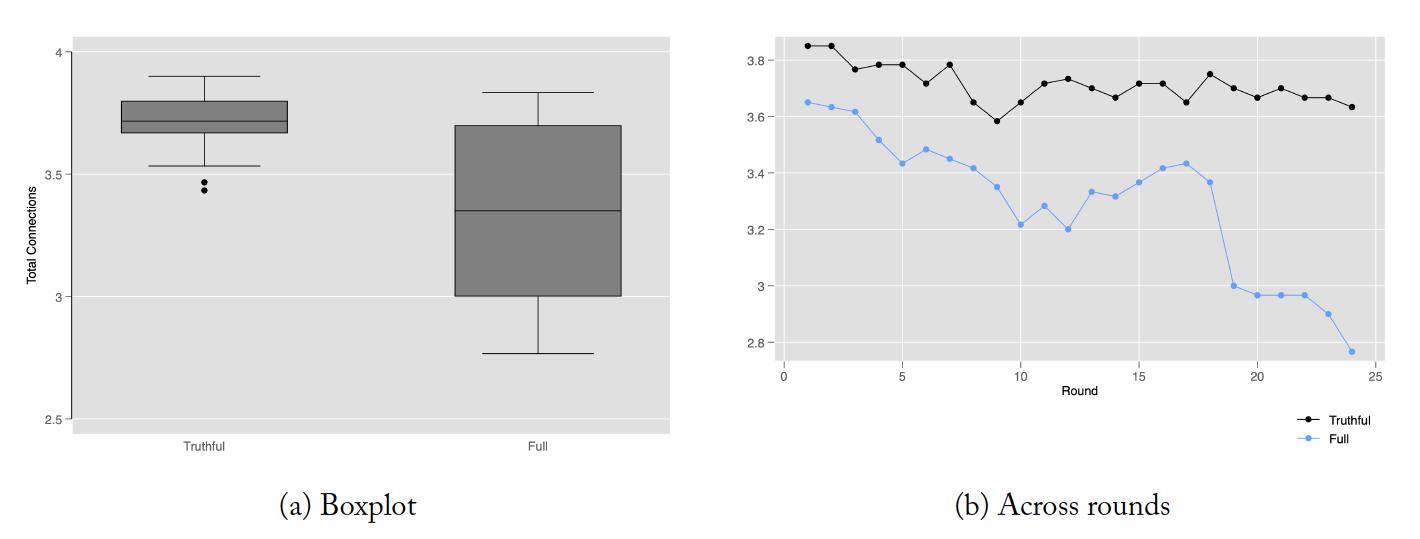
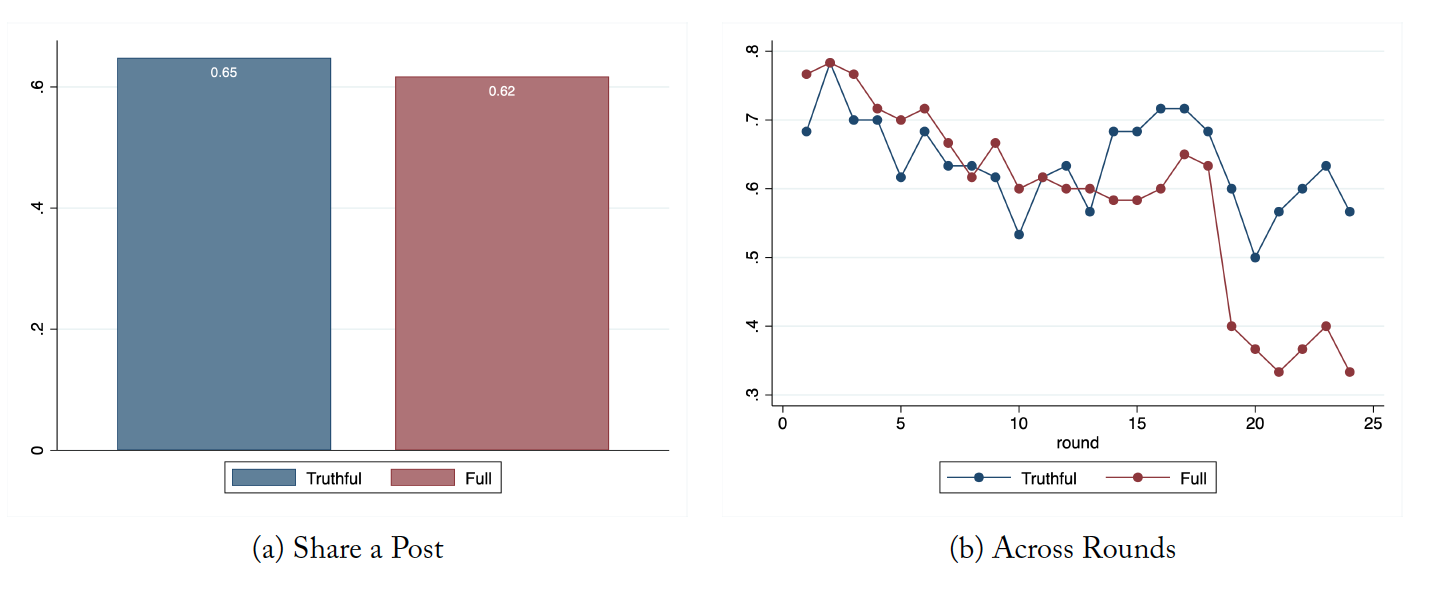
An individual can only see posts from group members they are following. The average number of people followed thus determines overall access and engagement with information shared on the social media platform. The average number of people followed by a group member is higher in the truthful information sharing protocol (Mann–Whitney, p < 0.001). Further, as illustrated in Figure 2b, allowing for the possibility of sharing misinformation leads to a decay in the number of people an individual chooses to follow.
Figure 2. Average number of group members followed on the social media platform
However, the number of group members making posts on social media does not differ by information sharing protocol (Mann-Whitney, n.s.). In the truthful information sharing protocol 65% of the group members share a post, while in the full information sharing protocol, 62% of the group members share a post. Across both protocols, over time, there is a downward trend in the proportion of group members sharing a post.18This is illustrated in Figure A1b in Appendix 5.
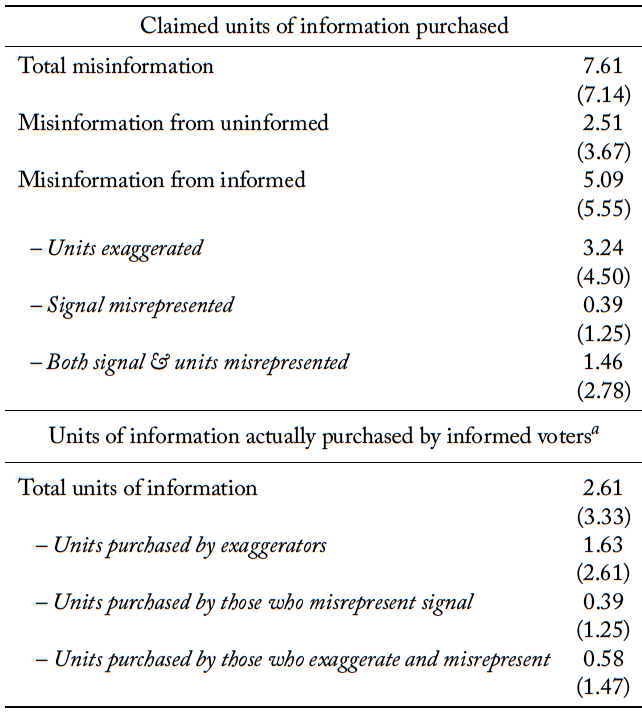
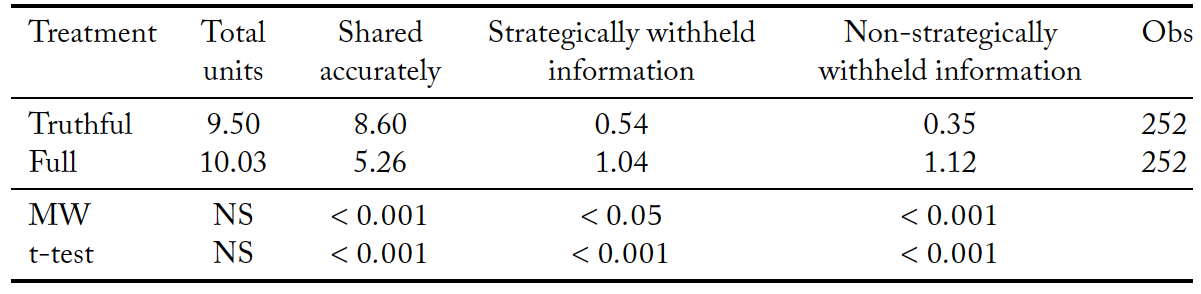
In Table 5 we decompose how individual information purchases are or are not shared on the social media platform. In the truthful information sharing protocol, over 90 percent of the information acquired is shared, compared to only 52 percent of the information when misinformation is permitted. This difference is statistically significant (Mann-Whitney, p < 0.001). More than one-fourth of the information purchased is inaccurately represented on the message board in the presence of misinformation.
Note that only a small proportion of information is strategically withheld across both the truthful and full information sharing protocols.19A unit of information is coded as strategically withheld if the color of the report does not concur with the partisan bias. One might expect that when users are constrained to post truthfully, the withholding of information would increase. We find exactly the opposite. More information is strategically withheld (Mann-Whitney, p < 0.05) and non-strategically withheld (Mann-Whitney, p < 0.001) in the presence of misinformation. That is, even when informed voters do not post misinformation, more information is not revealed to group members. This is indicative of the fact that some users seem to view information sharing as futile. Misinformation drives out truthful information sharing.
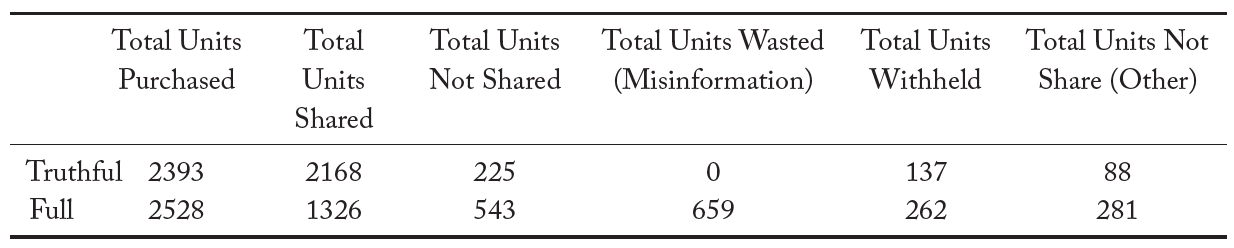
We now turn our attention to the source of misinformation. Table 5 contains summary statistics showing the level of misinformation being posted by informed and uninformed voters. For informed voters, we further decompose misinformation into three categories. In the first, voters simply exaggerate the number of units of information purchased, while truthfully revealing the color of their signal. In the second, voters accurately state the number of units of information purchased, but lie about the color of their signal. The third category captures those instances in which a voter misrepresented both the units of information purchased and the color of their signal. The second panel of this table details the information actually held by purveyors of misinformation.
Note that the source of 66.9% of the units of misinformation posted on the social media platform is informed voters. This misinformation displaces accurate information sharing, and is perhaps more pernicious. However, 64% of these units of misinformation involve informed voters who exaggerate the units they purchased, while truthfully revealing the color of their signal. Notice that the units of information actually purchased by those who exaggerate is about half the units they claim to have purchased.
Table 5. Composition of information shared
Strategically withheld: Information withheld if the color of the report did not match their partisan bias. Non-strategically withheld: Information not shared even when the color of the report matched their partisan bias.
Table 6. Decomposition of misinformation at the group level
Notes: Table contains means with standard deviations in parentheses. a Units actually purchased by purveyors of misinformation. This gives a measure of the units of information directly wasted due to misinformation.
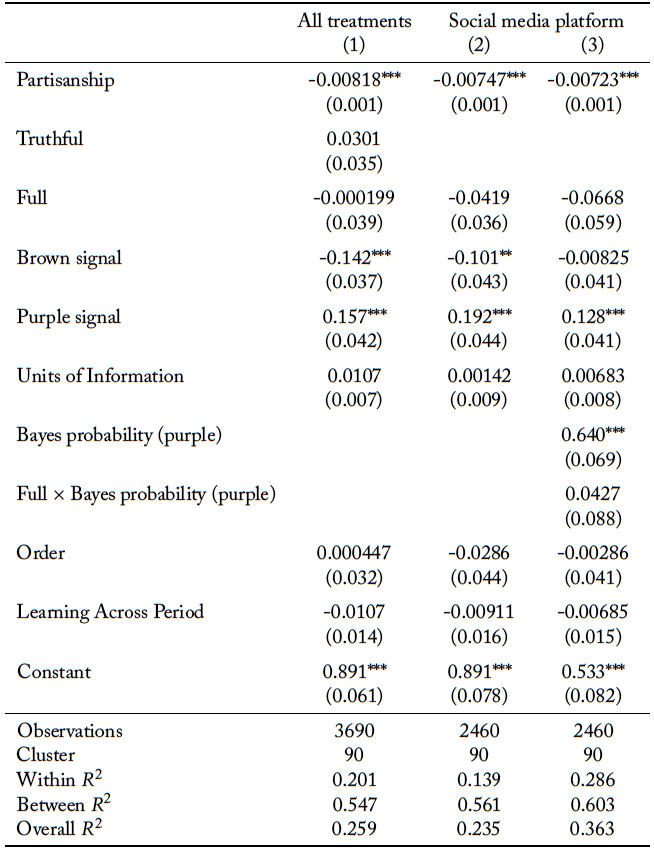
4.3 Regression analysis
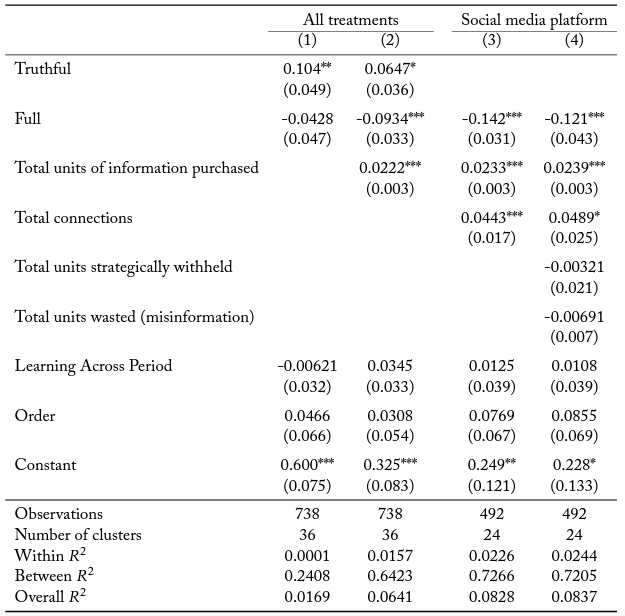
To further investigate the determinants of the quality of group decisions, we report panel linear probability models with robust standard errors clustered at the group level in Table 7.20Logistic and probit regression models yield comparable results. The dependent variable of interest is whether the group’s vote matched the state of the world. In columns 1 and 2, we include data from all the information sharing protocols. The independent variables include dummy variables corresponding to the two information sharing protocols, so that the excluded category is the case of no social media. We also include a variable to control for the order in which the protocol was introduced, and a variable to account for learning across periods.21The variable used to pick up order effects is a dummy variable for whether or not the information sharing protocol (or lack thereof ) was the first protocol a subject participated in. Learning across periods is controlled for via log(t − 1). In column 2, we also control for the total units of information purchased by the group. In columns 3 and 4, we exclude data from the baseline treatment without social media, to isolate the effect of misinformation conditional on the presence of the platform. We include a dummy variable for the full information sharing protocol. In column 3, we control for the total units of information purchased by the group, as well as the total number of connections within a group, to measure engagement with the social media platform. We also control for learning across periods. In column 4, we additionally control for two variables that capture the total information purchased that is not truthfully shared on the social media platform. First, we control for the number of units of information that is strategically withheld. Second, we account for the units of information wasted due to misinformation.
Relative to the case of no social media, the truthful information sharing protocol increases the overall quality of group decisions. Recall that social media induces groups to purchase more units of information. Even when we control for the total units of information purchased, there is still statistically significant improvement. Interestingly, the full information sharing protocol does not significantly differ from the baseline, unless we also control for the total units of information purchased, after which it does significantly worse. That is, in the presence of misinformation, the quality of group decisions is worse relative to the case of no social media, once the level of information purchased by a group is accounted for. Groups in the presence of misinformation end up purchasing more information without improving their quality of decision making.
In columns 3 and 4, we only analyze the data from the two information sharing protocols. Relative to truthful communication, the presence of misinformation lowers the quality of decision making even after controlling for the units of information purchased and the number of connections. Recall that misinformation erodes the total number of connections on the social media platform. The regression results corroborate this finding. An increase in the total number of connections improves the quality of outcomes. This effect is still significant even when we control for the nature of the information shared on the social media platform. Both withholding information and information lost to misinformation lowers the quality of decision making but the corresponding coefficients are not statistically significant.
Table 7. Quality of group decision making
Robust standard errors in parentheses clustered at the group level. *p<0.10, **p<0.05, ***p<0.01
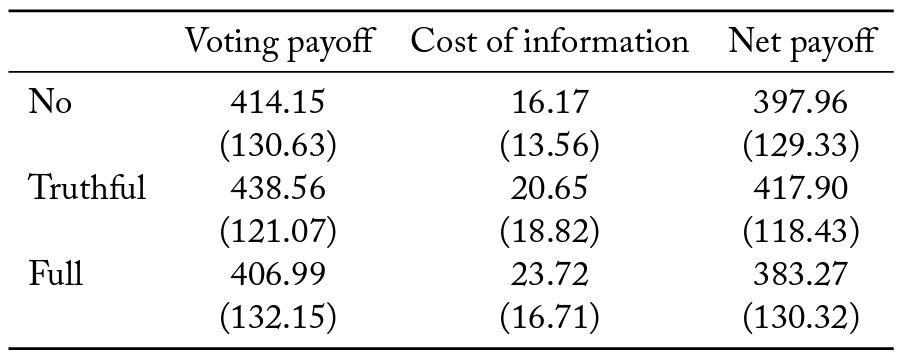
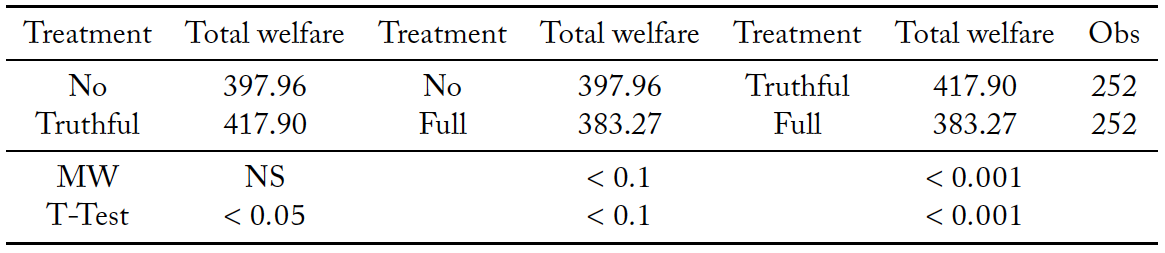
Next, we turn our attention to the welfare implications of group decisions. We specify the social welfare function to be the sum of all the subjects’ net payoffs within a group. In Table 8 we decompose payoffs as the sum of the payoff from voting and the cost of purchasing information. Groups in the full information sharing protocol have the lowest income from voting and pay the highest cost for information acquisition. This is reflected in a lower net payoff relative to the case with truthful information sharing (Mann-Whitney, p < 0.001), and the scenario without a social media platform (Mann-Whitney, p < 0.1). However, there is no significant welfare difference between the truthful information sharing protocol and the baseline with no information sharing (Mann-Whitney, n.s).
Table 8. Summary statistics of payoffs
Notes: Table contains means with standard deviations in parentheses.
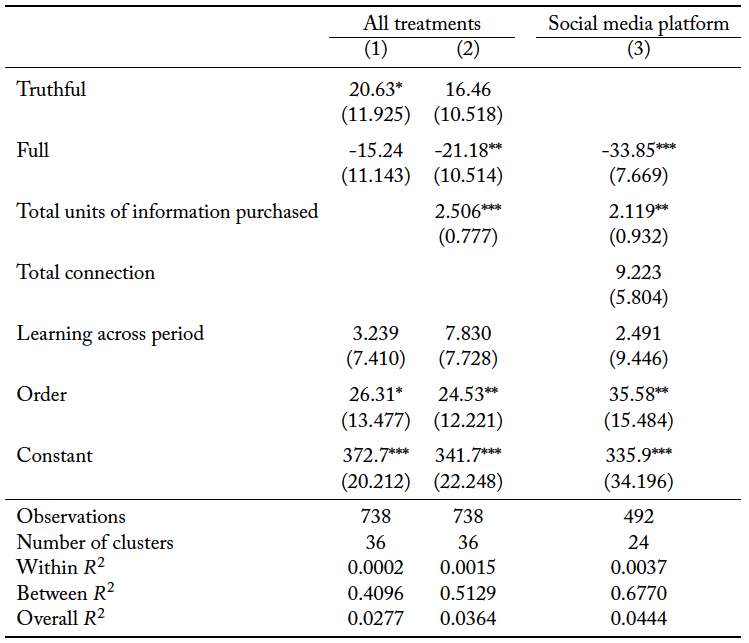
We also report regression results that analyze the effects of the social media platform and misinformation on total welfare. Results of panel linear regression models with robust standard errors clustered at the group level are reported in Table 9. The regression analysis allows us to control for learning across periods and the order in which the information sharing protocol was introduced. The dependent variable is the net payoff in each round. Columns 1 and 2 include data from all the information sharing protocols. The independent variables include dummy variables corresponding to the two information sharing protocols, so that the excluded category is the case of no social media. In column 2, in addition to order and learning across periods, we control for the total units of information purchased by the group. In column 3, we exclude data from the treatment without social media. We include a dummy for the full information sharing protocol. We control for the total units of information purchased, the total number of connections on the social media platform, and learning. Finally, we control for order effects.
Relative to the absence of social media, there is an improvement in net payoffs when posts are limited to be truthful, although this is only marginally significant. In fact, once we control for the total information purchased, this effect is not significant. This is interesting, as it demonstrates that the increase in the quality of group decision making afforded by a social media platform without misinformation does not significantly improve welfare. Even if misinformation is successfully curtailed, social media is unlikely to yield welfare gains.
In the presence of misinformation, once we control for the total information purchased, groups have lower net payoffs relative to the absence of social media. That is, groups in the presence of misinformation purchase more information, but this does not result in higher net payoffs. In column 3, we find a similar result when conditioning on the presence of social media. Misinformation yields lower net payoffs relative to the scenario when only truthful messages can be shared, even after we have controlled for both the total information purchased and connections on the social media platform.
Table 9. Total welfare
Robust standard errors in parentheses clustered at the group level. * p<0.10, ** p<0.05, *** p<0.01
4.4 Individual level analysis
In each round individuals make a series of decisions. In the absence of social media, individuals decide how much information to purchase and then decide which color to vote for. When social media is present, the decisions are how much information to purchase, whom to follow on the social media platform, the contents of their post (if any), and which color to vote for. In what follows, we analyze each of these decisions separately.
4.4.1 Information purchase
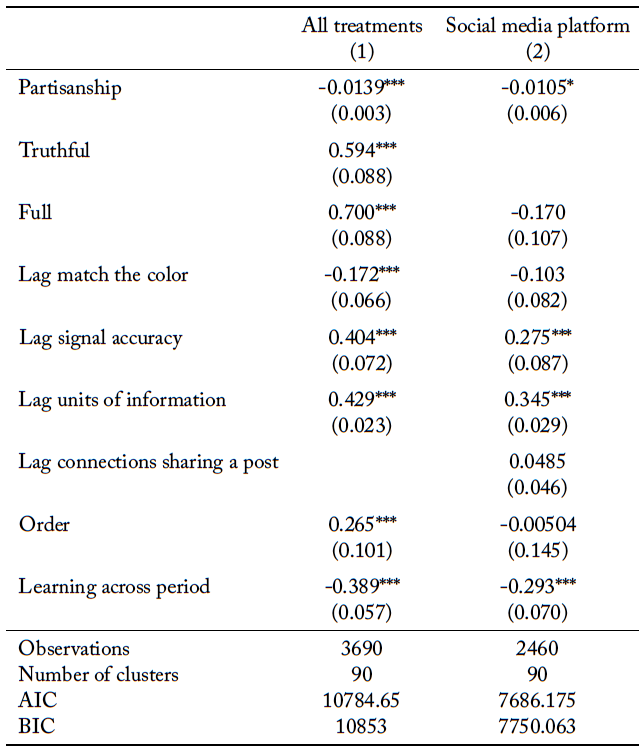
What determines how many units of information an individual decides to purchase? We investigate this using a panel Tobit regressions, and the results are reported in Table 10. The dependent variable is the units of information purchased, which can be any integer between 0 and 9, inclusive. In column 1, we include data from all treatments, both with and without information sharing. We consider the following independent variables of interest: the degree of partisanship, dummy variables corresponding to the two information sharing protocols (so that the excluded category is the case of no social media), whether the group’s vote matched the state of world in the previous period, whether the subject’s signal matched the state of the world in the previous period, and the number of units of information the subject purchased in the previous period. In addition, we control for the order in which the protocol was introduced and for learning across periods. In column 2, we exclude data when there is no social media, so that we exclusively consider the effect of allowing misinformation on a social media platform. In addition to the variables included in the preceding column, we include a dummy variable which is equal to one if a participant is in the full information sharing protocol as well as a variable for the total number of posts an individual saw on the social media platform in the previous period.
We find an inverse relationship between the degree of partisanship and the units of information purchased. Individuals who have extreme values of p purchase less information. This is not surprising, since more extreme voter types have no incentive to condition their vote on the realization of their signal.
Interestingly, individuals buy more units of information in the presence of a social media platform. In fact, focusing on the results from column 2, note that the increase in individual information acquisition does not depend on whether or not misinformation is permitted on the social media platform; social media leads to an increase in information acquisition, even when users are assured that all posts will be accurate. Thus, concerns that social media, which is potentially rife with misinformation, will crowd out information acquisition are unfounded.
Note that there is a positive relationship between previous and current units of information purchased by an individual. Further, if an individual’s signal was accurate in the previous period, they increase the number of units of information they purchase in the subsequent period. Thus, if information is observed to be useful (correct), then individuals purchase more of it in the next period.
When their group was successful in matching the state of the world in the previous period, an individual responds by lowering the units of information they purchase in the current period. However, this effect is not significant when analyzing data from the two information sharing protocols with a social media platform. Further, in the presence of a social media platform, individuals purchase more units of information if more of their connections shared a post in the previous period.
Table 10. Information purchase
Robust standard errors in parentheses. Average marginal effects reported. * p<0.10, ** p<0.05, *** p<0.01
4.4.2 Decision to follow on social media platform
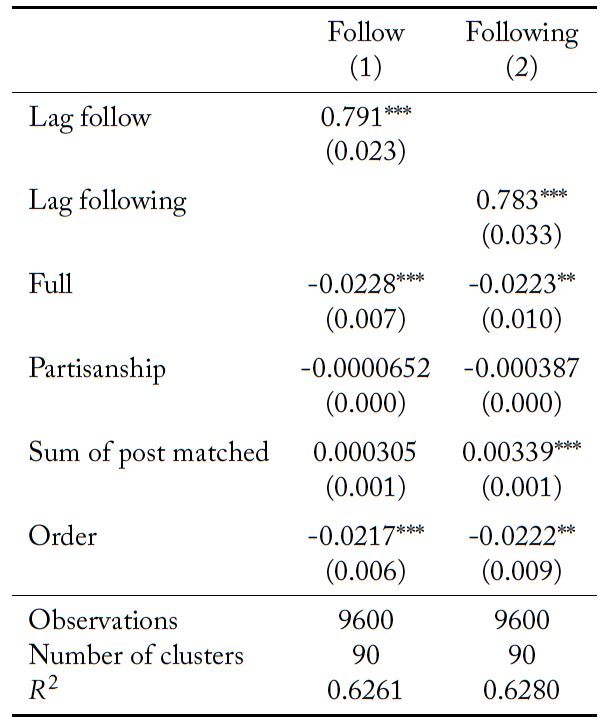
After observing their signals, each individual chooses whether or not to follow each member of their group on the social media platform. We are interested in the decision to follow another group member, as well as when group members decide to follow a given individual. To investigate these decisions, we use linear probability models on the dyadic data set that corresponds to all possible connection decisions in each period. The results are reported in Table 11.22Logistic regression models yield predictions which are qualitatively similar. Results are available on request. In column 1 the dependent variable is a dummy variable for whether individual i decides to follow each group member j in period t. In column 2, the dependent variable is a dummy variable for whether each of the other members of individual i’s group decide to follow him/her in period t. That is, in period t there are four observations for each individual i.
The independent variables of interest for both column 1 and 2 are the following: a dummy variable for the full information sharing protocol (so that the excluded category is the truthful information sharing protocol), the lag of the dependant variable, the degree of partisanship, the number of previous posts made by the relevant individual which matched the state of the world, and the order in which the protocol was introduced.
In the first column, which focuses on an individual’s decisions about whom to follow, we find strong path dependency. Individuals who follow a group member in the previous period are more likely to follow them in the current period. Interestingly, an individual is less likely to follow any given group member when misinformation is permitted on social media. That is, the possibility of misinformation reduces the number of connections on social media. Note that an individual’s degree of partisanship has no significant effect on their following decisions.
These findings are consistent with the group level observation that there are fewer connections in the presence of misinformation. In our group level analysis we showed that the presence of fewer connections is critical to explaining the lower quality of group decision making when misinformation is permissible.
The results from column 2 of Table 11, which focus on the decision of a group member to follow an individual, are largely consistent with the results described in column 1. The only difference of note is that the number of posts made by an individual which match the state of the world leads to a statistically significant increase in the number of followers.
Table 11. Probability of following others on the social media platform
Robust standard errors in parentheses. * p<0.10, ** p<0.05, *** p<0.01
4.4.3 Posts shared
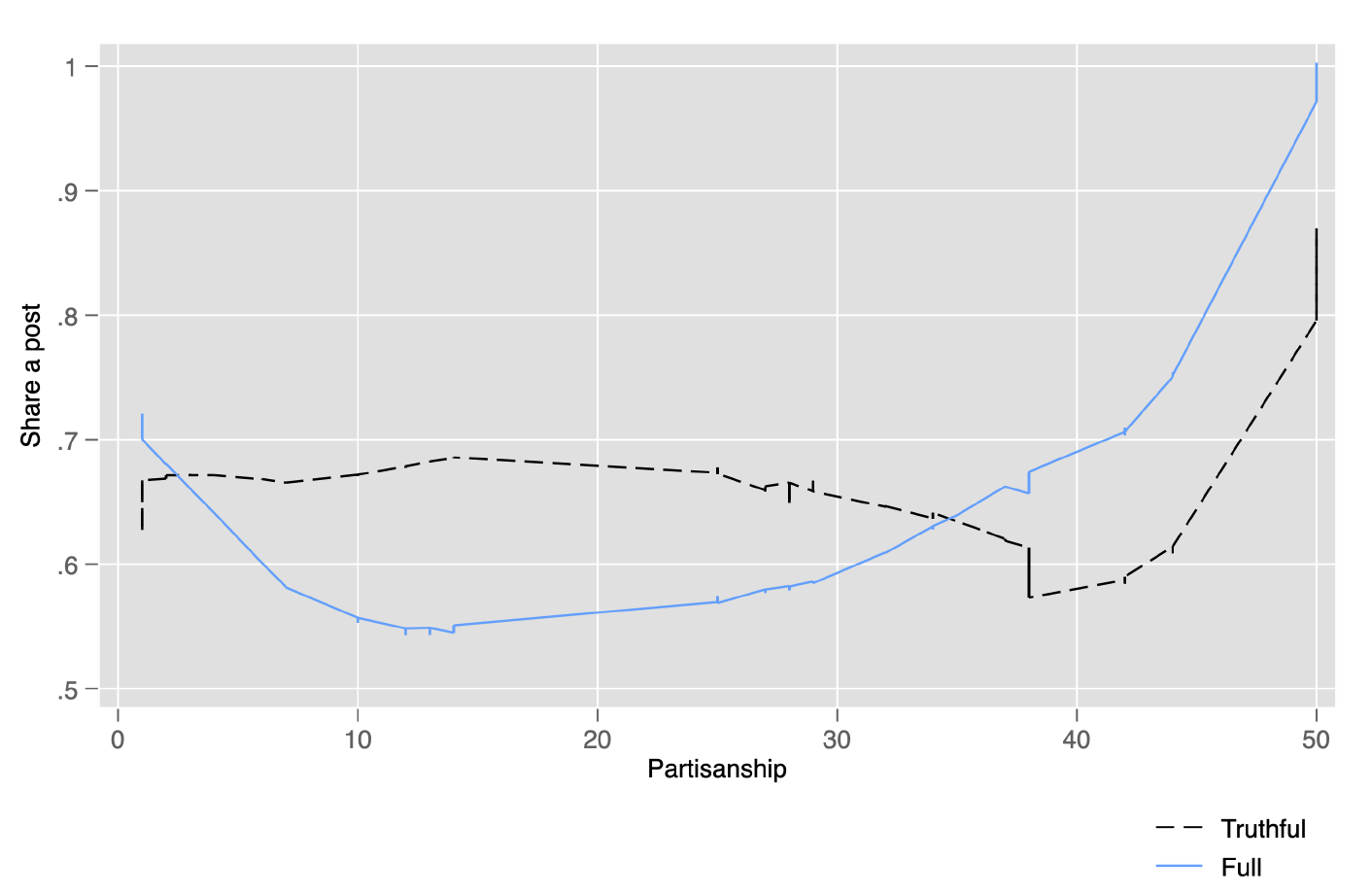
Posts are critical to the process of information aggregation on the social media platform. However, sharing a post is voluntary. Figure 3 plots locally weighted regression estimates of the likelihood of sharing a post on the degree of partisanship. Relative to the full information sharing protocol, individuals with a lower degree of partisanship appear to be more likely to share a post.
Figure 3. Likelihood of sharing a post by degree of partisanship
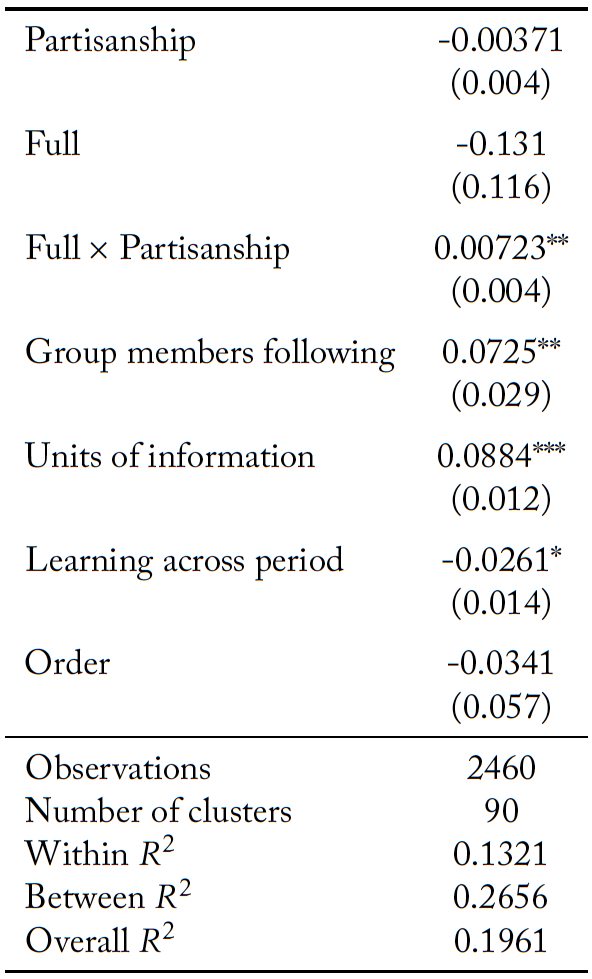
We explore this further in a panel linear probability model with standard errors clustered at the individual level. The results of this analysis are reported in Table 13.23Logistic regressions yielded similar predictions. These results are available upon request. The dependent variable is a dummy variable that is equal to one if individual i decides to share a post in period t. The independent variables of interest are the degree of partisanship, a dummy variable for the full information sharing protocol, an interaction term between the full information sharing protocol and the degree of partisanship, the number of group members following individual i in period t, the number of units of information purchased by individual i in period t. In addition, we control for order effects and learning across periods.
Table 12. Probability of sharing a post
Standard errors in parentheses. * p<0.10, ** p<0.05, *** p<0.01
In line with the findings at the group level, there is no statistically significant difference in the likelihood of sharing a post between the truthful and full information sharing protocols. When misinformation is permissible, individuals with a higher degree of partisanship are more likely to share a post. However, this is not true when posts must be accurate. Interestingly, an individual who purchases more units of information is more likely to share a post. Further, individuals with more followers are more likely to share a post; this is not surprising, since the information shared can potentially influence the group’s outcome.
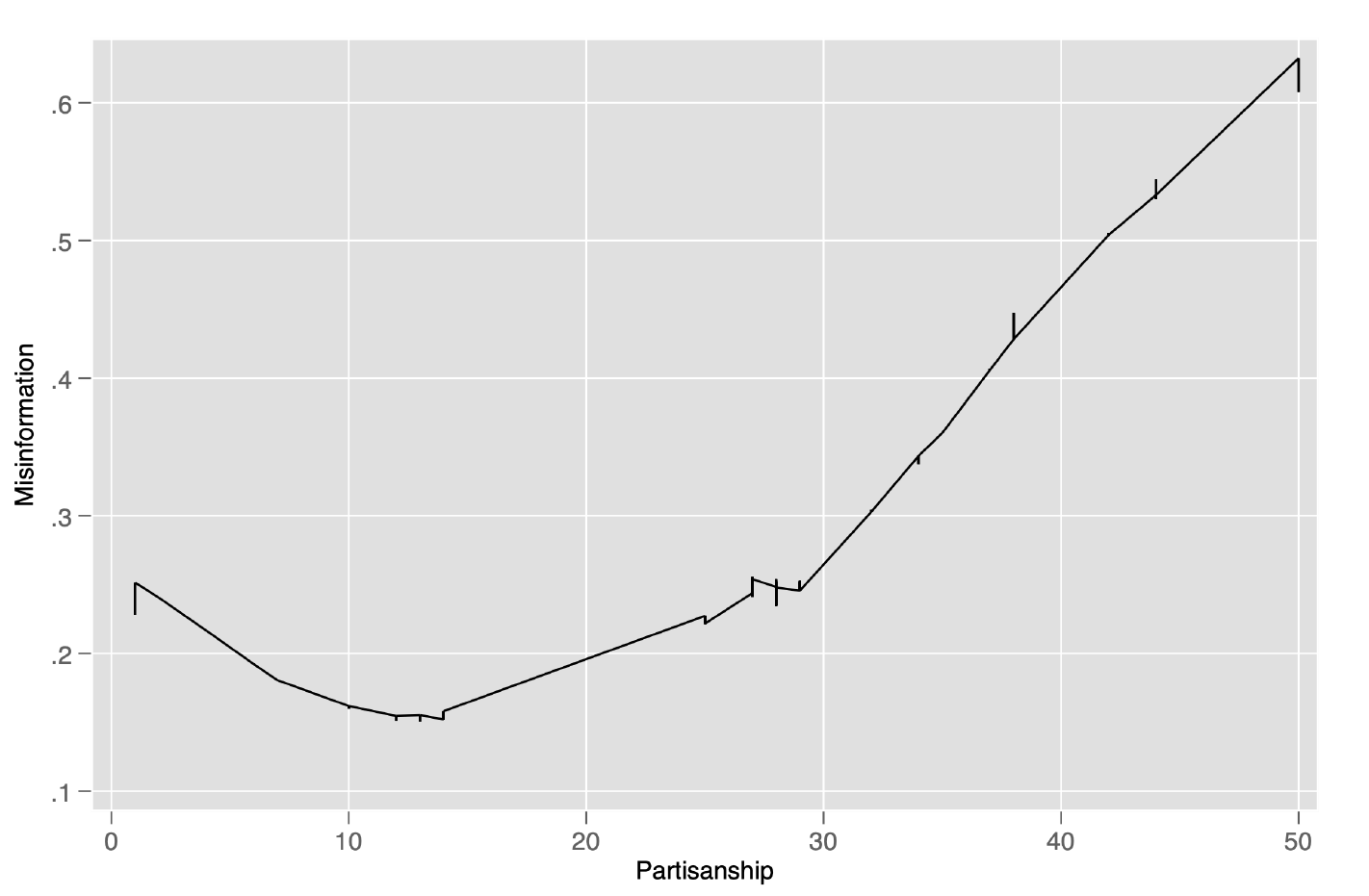
The degree of partisanship is associated with an increased likelihood of making a post only when it is possible to post misinformation. This suggests that those with an incentive to post misinformation take the opportunity when it is presented. To investigate this, Figure 4 plots locally weighted regression estimates of the likelihood of sharing a post containing misinformation on the degree of partisanship. As the degree of partisanship increases, individuals appear more likely to share a post containing misinformation. This can partly explain the lower quality of group decision making in the full information sharing protocol.
Figure 4. Posts containing misinformation by partisanship
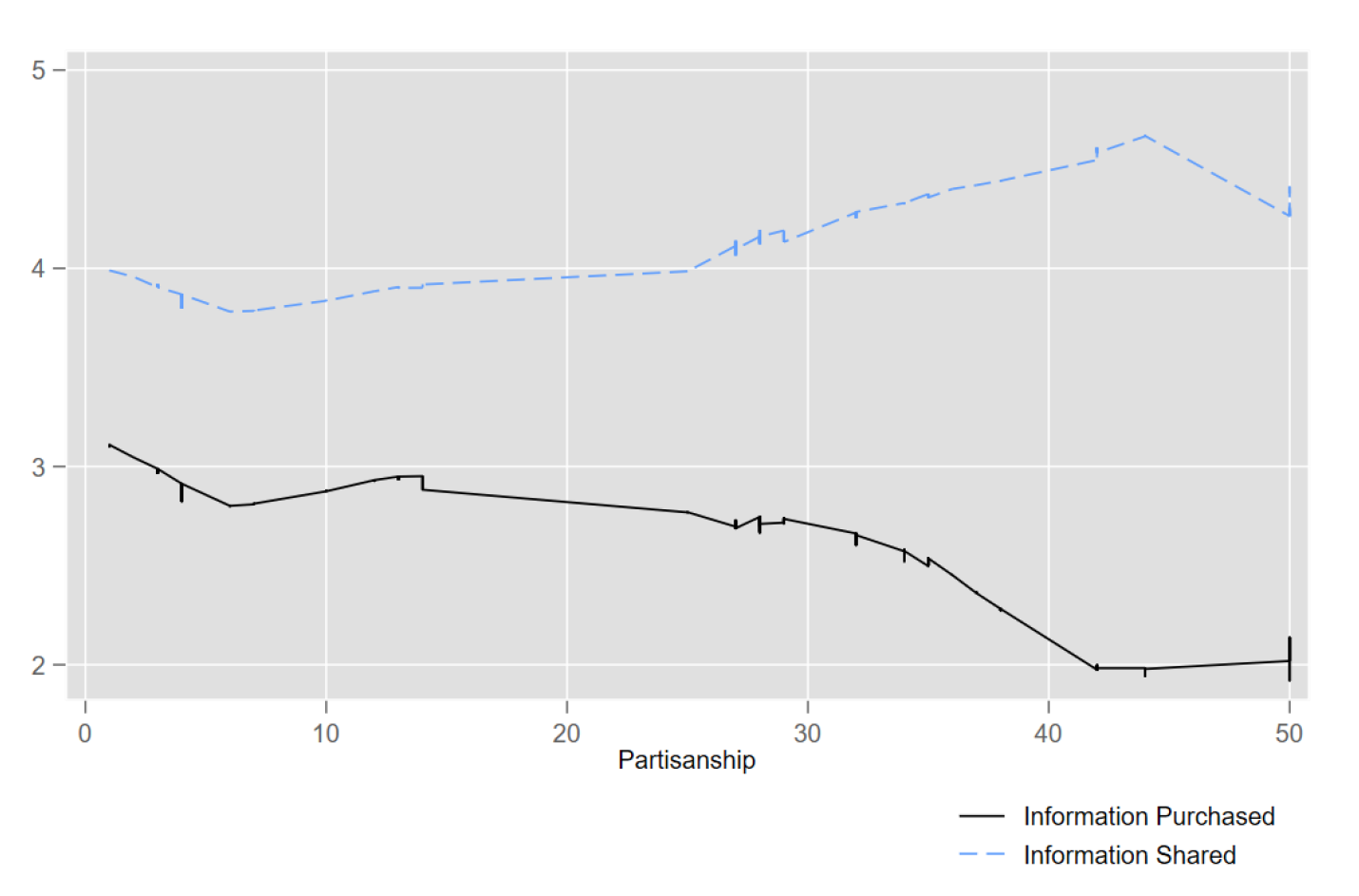
A post contains two critical pieces of information relevant to the voting decision. The first is the number of units of information purchased, and the second is the color of the signal. Figure 5 plots locally weighted regression estimates of the number of units of information shared and the information purchased by the degree of partisanship, restricting attention to the full information sharing protocol, where these are permitted to differ. As the degree of partisanship increases, individuals increase the degree to which they overstate the number of units of information they purchased.
We explore this further in a Tobit regression analysis in which the dependent variable is the difference between the number of units of information reported and the number of units of information actually purchased. We control order effects and learning across periods. The results are reported in Table 13. Even after we control order effects and learning across periods, we find that as the degree of partisanship increases, the degree to which individuals overstate the number of units of information purchased in their posts also increases.
Figure 5. Number of units of information reported
Table 13. Units of information reported
Marginal effects; Standard errors in parentheses. * p<0.10, ** p<0.05, *** p<0.01
Figure 6. Color reported
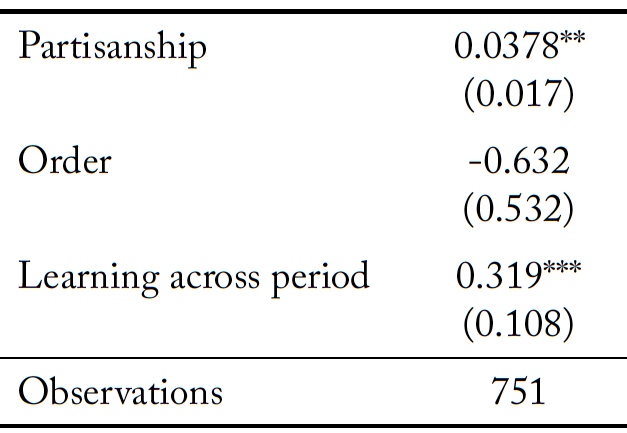
Overstating the number of units of information purchased can be seriously detrimental to the information aggregation process. This is especially true when coupled with misrepresentation of the color of the signal. Figure 6 reports locally weighted regressions of the likelihood of reporting that the received signal was either Brown (panel 1) or Purple (panel 2) by partisanship. Note that in this figure we condition on p, rather than the distance between p and 50. As p increases, individuals are more likely to report the color that matches their partisan preferences.
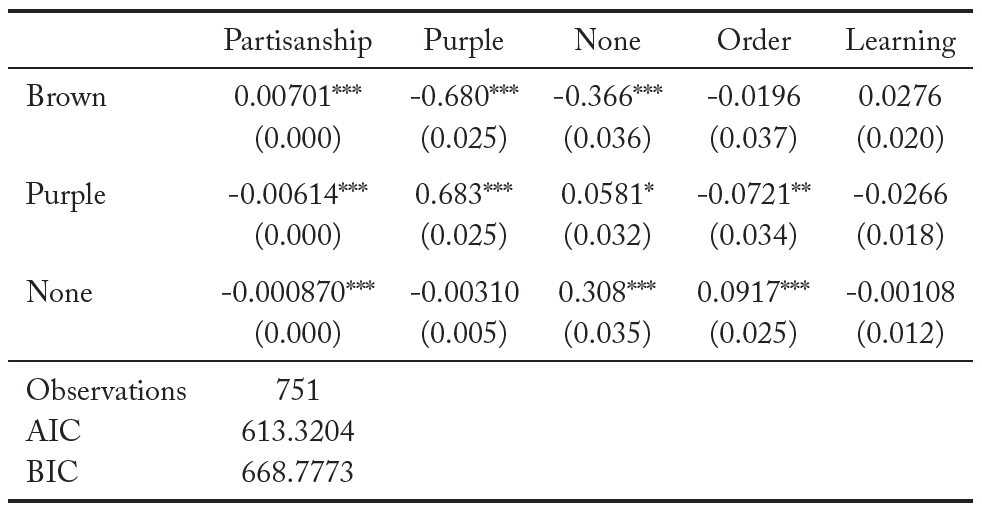
We explore this further in a multinomial logistic regression. The dependent variables of interest are the three possible options an individual can report: Brown, Purple, and None. The independent variables of interest are their type, (p), and dummy variables that are equal to one if the individual got a Purple signal and when the individual does not purchase any units of information and gets a “none” signal, respectively. Thus the excluded category is when the individual gets a Brown signal. We control for order effects and learning across periods. The results of the regression analysis are reported in Table 14.
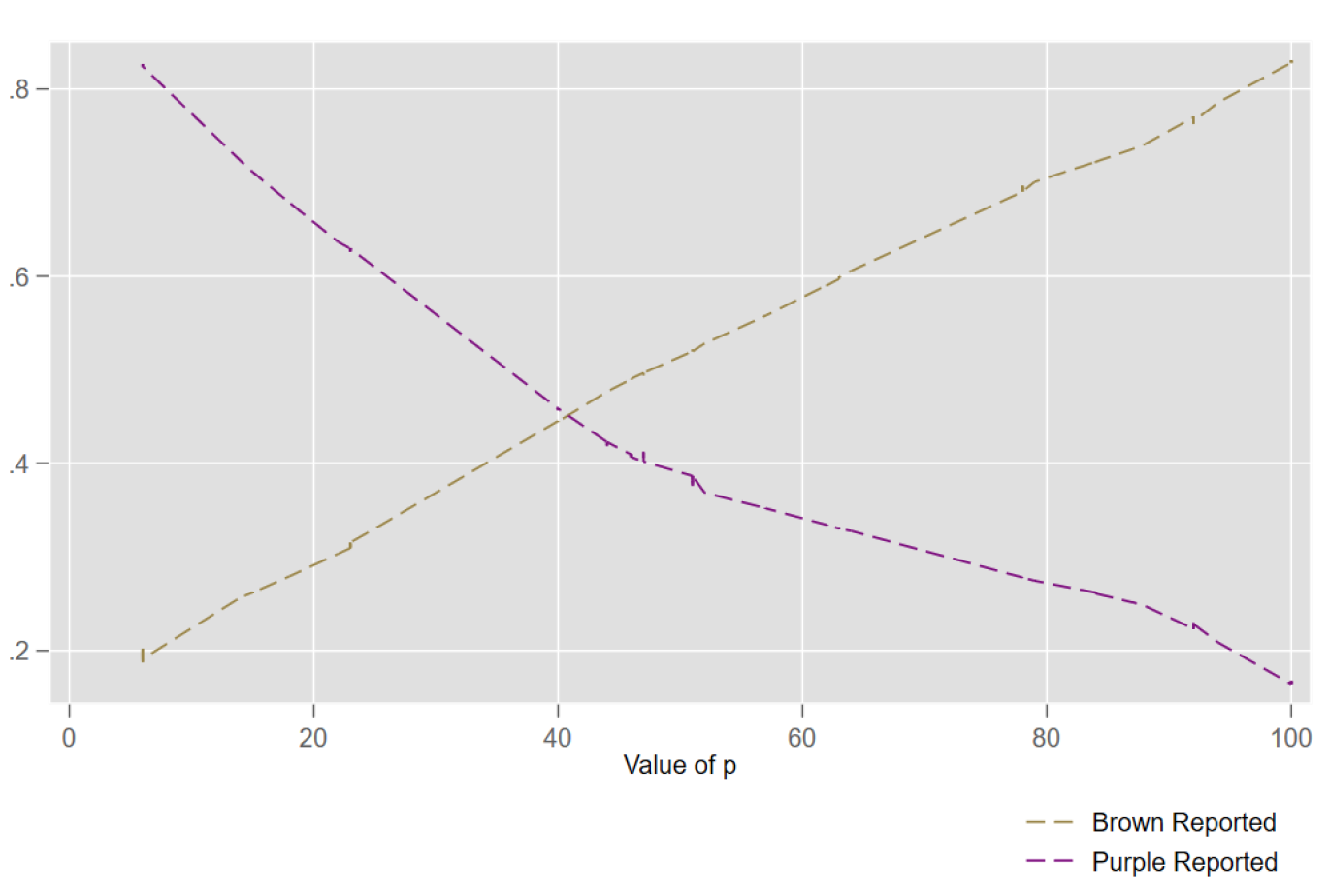
We find a positive relationship between the value of p and the likelihood of reporting Brown, and a negative relationship between the value of p and reporting Purple. That is, individuals misrepresent the color of the report based on their partisan preferences even after we control for the color of the signal received, order effects and learning across periods.
Table 14. Multinomial logistic regression
Marginal effects; Standard errors in parentheses * p<0.10, ** p<0.05, *** p<0.01
4.4.4 Voting decision
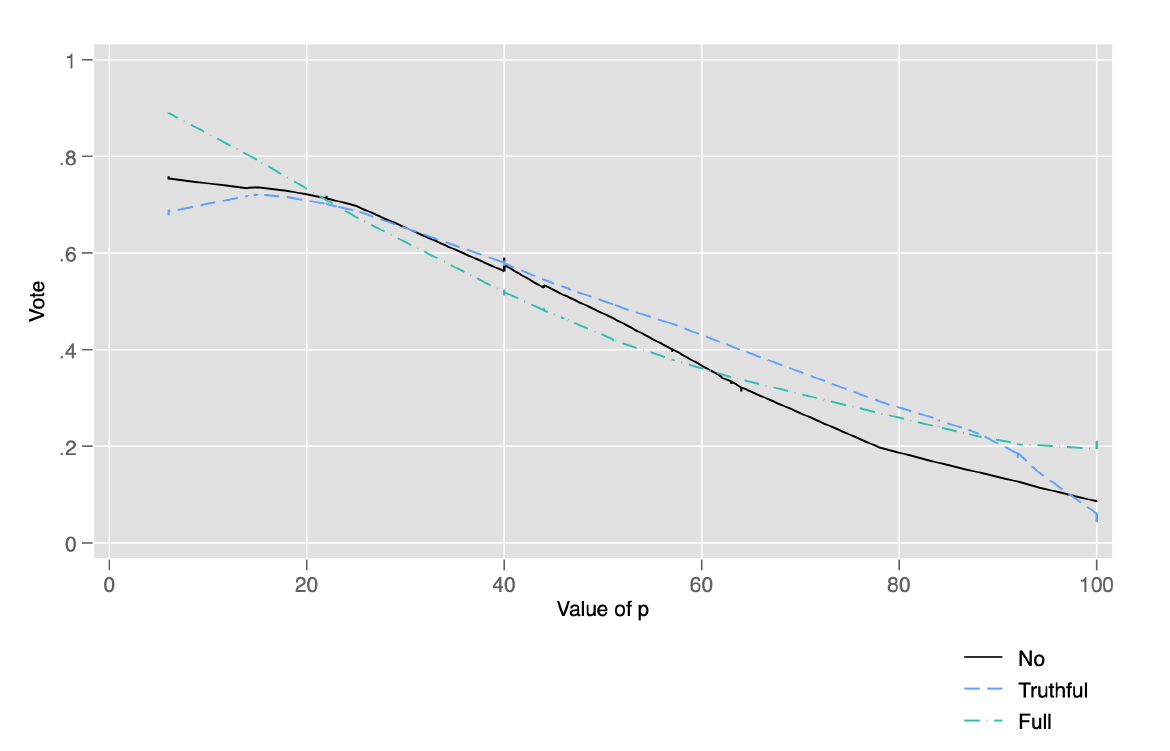
Figure 7. Voting decision
Figure 7 plots locally weighted regression estimates of the likelihood of voting for Purple (1) or Brown (0) over the degree of partisanship. There is a clear relationship between the value of p and the probability of voting in line with their partisan preferences. Apart from partisanship, we explore other factors that influence an individual’s voting decision in a linear probability model; the results from the regressions are reported in Table 15. The dependent variable of interest is the dummy variable which takes value 1 if the individual votes for Purple and 0 if he or she votes for Brown.
In column 1 we include data from the three information sharing protocols. The independent variables of interest include partisanship (p), dummy variables for the truthful and full information sharing protocols, so that the excluded category is the case of no social media. We also include dummy variables corresponding to whether the individual got a Brown or Purple signal, so that the excluded category is the case where the individual did not purchase information and did not get a signal. In addition, we control for the number of units of information purchased, order effects, and learning across periods.
In column 2, we exclude the data from the baseline treatment without a social media platform in order to isolate the effect of misinformation on social media. The independent variables are similar to those of column 1, except that there is only a dummy variable for the full information sharing protocol (so that the excluded category is the truthful information sharing protocol). In column 3, we again focus on data from the treatments with social media. In addition to the independent variables in column 2, we add the probability that the state of the world is Purple, under the assumption that all posts observed by the individual are taken as truthful, and that individuals are Bayesian. We interact the aforementioned Bayesian probability and the full information sharing protocol to test whether there are any differences in how information is perceived when misinformation is permissible.
Focusing on the analysis with all three treatments (column 1), note that there is a negative relationship between partisanship and voting for Purple. That is individuals with higher value of p are more likely to vote for Brown, as would be expected. Not surprisingly, the information sharing protocol has, on average, no effect on an individual’s likelihood of voting for Purple. The color of an individual’s realized signal is, also not surprisingly, a statistically significant determinant of their vote, with the expected signs.
Interestingly, the number of units of information purchased is not significant. Turning attention to column 2, where we exclude data without social media, the results of the analysis are largely unchanged, which demonstrates that voting behavior does not dramatically change in the face of social media.
In column 3, we control for the probability that the state of the world is Purple. Interestingly, the corresponding coefficient is positive and highly significant. Note however, that it is less than one, indicating that individuals underweight the available information when making voting decisions. Importantly, the interaction of this probability with the full information sharing protocol is insignificant. That is, individuals do not seem to discount the available information when it is possible that some of it is misinformation. That said, the decision to follow other group members (and thus to see their posts) is endogenous.
Table 15. Voting decision
Standard errors in parentheses * p<0.10, ** p<0.05, *** p<0.01
5 Conclusion
Social media platforms have fundamentally changed the way we interact with others and how we gather information. An individual’s ability to use the platforms to influence voters’ information is currently at the forefront of political discourse. The focus of that discourse has been on the prevalence of misinformation and how partisan biases effectively mobilize opinions. However, little is yet known about how partisanship influences the nature of information shared on the social media platform. In our experiment, we study how the nature of information shared on a social media platform influences voting outcomes and welfare.
We report the results of an experiment in which subjects can purchase information about an unobserved, binary state of the world. After information is gathered, the group votes for one of the possible states. Each individual receives a fixed payoff if the group vote matches the state. A further payoff is awarded to an individual if the group votes for a given state. For each individual, the magnitude of this partisan payoff is an i.i.d. draw from a common knowledge distribution.
We consider three information sharing protocols. In the first, there is no social media platform, and any information purchased cannot be shared. The only way subjects can learn about the underlying state of the world is via information they purchase themselves. In the second, social media is present, and any group member has the option to post the information they purchased. Note that posts are constrained to be truthful. Group members decide which of their group members they would like to follow, where following a group member allowed them to observe any post of said member. In the third, the social media platform exists, but posts need not be truthful. In the information sharing protocol where a social media platform is present there are two ways to learn about the underlying state of the world. First, subjects can purchase information. Second, subjects can learn from the information shared on the social media platform.
Our results show that the presence of social media can increase the quality of group decision making. Importantly, this is only true when misinformation is not permitted. Interestingly, the presence of social media leads to higher levels of costly information acquisition, regardless of whether or not misinformation is permissible. Thus, the lower quality of decisions due to the presence of misinformation is not due to a less informed electorate. In fact, when misinformation is permissible, the increase in informedness is accompanied by a decrease in the quality of group decision making.
Another key insight is that, conditional on the presence of social media, the possibility of sharing a post containing misinformation reduces the average number of connections on the platform. This is a key mechanism to explain the reduction in the quality of decision making. More importantly, in our view, this demonstrates that the effects of misinformation are likely to affect the profitability of social media platforms themselves. That is, if social media platforms do not police misinformation, they should expect to see lower levels of platform engagement, as measured by the connectedness of their users.
Our results highlight the need for additional research into what content moderation policies are effective at combating misinformation. Is it important to fact-check all posts, or is it sufficient to fact-check a portion of them? Are purveyors of misinformation deterred by the prospect of having their posts labeled as misinformation, or is it necessary to impose consequences that persist over time? Research addressing these questions is of pressing importance.
Second, we observe that just the presence of a social media platform induces individuals across the partisan spectrum to purchase more units of information. It is crucial to explore the social norms governing the purchasing and sharing of information on a social media platform in future research. Do content moderation policies influence the social norms around posting misinformation? Can individuals be nudged to verify before sharing posts to minimize the spread of posts containing misinformation?
Another area of future research is to study the source of biased signals. In our experiment, the signals are not biased. The results from Pogorelskiy and Shum (2019) demonstrate that biased signals can be detrimental to the voting process. It is important to focus on factors that lead to biased signals. For instance, does competition among media outlets lead to better signals quality?
Appendix A: Instructions
Welcome
Once the experiment begins, we request that you not talk until the end of the experiment. If you have any questions, please raise your hand, and an experimenter will come to you.
Payment
For today’s experiment, you will receive a show-up fee of $5. All other amounts will be denominated in Experimental Francs (EF ). These Experimental Francs will be traded in for Dollars at a rate of 145EF = $1.
Stages
This experiment will be conducted in two stages. At the beginning of each stage:
- Five individuals from the room would be randomly matched to form a
- Each group member will be randomly assigned a Subject ID – A, B, C, D, or E.
- Each group member will be assigned a whole number, p, which is randomly chosen between 0 EF and 100 EF. Any number between 0 EF and 100 EF has the same chance of being selected. It is independently drawn for each group Therefore, the draw of p for one group member is not affected by those of the other members of the group. Each group member knows their own p, but not those of the other group members.
In each stage, everyone in the group will make decisions for at least 5 rounds. There is a 90% chance there will be a sixth round. If there is a sixth round, there is a 90% chance there will be a seventh round, and so on. Thus, at the end of each round (after the fifth round) there is a 90% chance that there will be at least one more round.
You can think of this as the computer rolling a 10 sided dice at the end of each round after the fifth round. If the number is 1 through 9 there is at least one more round. If the number is 10 then the stage end.
Round overview
Each round will consist of the following sequence:
- Jar Assignment: Each group is randomly assigned either a Brown Jar or a Purple The color of the jar will not be known by any group member.
- Buying Information: Each group member has the option to buy information about the color of the Jar that has been randomly assigned.
- Connections: Each group has a message Each group member has the option to follow other members of the group on this message board.
- Post Choice: After making connection decisions, each group member will have a choice regarding whether or not to post information.
- Post Creation: Each group member who has opted to post information determines the content of their post for the message board.
- Viewing posts on the message board: Each group member will observe the posts of those group members they have connected with, provided they have decided to make a
- Vote: Each group member casts a vote for either Brown or The color that gets three or more votes is the group decision.
Decision Environment & Choices
All treatments
Jar Assignment
At the beginning of every round, the computer will randomly assign one of two options as the correct Jar for each group: the Brown Jar or the Purple Jar. In each round, there is a 50% probability that the Jar assigned to a group is the Brown Jar and a 50% probability that the Jar assigned to a group is the Purple Jar. The computer will choose the Jar randomly for each group and separately for each round. Therefore, the chance that your group is assigned the Brown Jar or the Purple Jar shall not be affected by what happened in previous rounds or by what is assigned to other groups. The choice shall always be completely random in each round, with a probability of 50% for the Brown Jar and 50% for the Purple Jar.
Voting Task
Each group member will decide between one of the two colors: Brown or the Purple. Specifically, at the end of each round, the group will simultaneously vote for either Brown or Purple. The group decision will be determined by the color which gets three or more votes.
Payoff from voting
The payoff from voting that each group member earns in the round depends on the outcome of the vote. There are two parts to this payoff.
Part A
Remember that at the start of each stage, each group member is assigned a whole number, p, which is randomly chosen between 0EF and 100EF. Any number between 0EF and 100EF has the same chance of being selected. It is independently drawn for each group member. Thererore, the draw of p for one group member is not affected by the draw of p of the other members of their group. Each group member knows their own p, but not those of their other group members. Remember that the value of p assigned to each group member remains fixed within each stage but is randomly assigned in each stage.
Each group member gets p EF if the group votes for Brown, and 100 – p EF if the group votes for Purple. This payoff does not depend on the color of the Jar,which is randomly assigned at the start of each round. Notice that this means that each group member is likely to get a different payoff if Brown wins the vote because each group member is likely to have a different p. Similarly, each group member is likely to get a different payoff if Purple wins the vote.
Part B
If the color chosen by the vote matches the color of the Jar that was randomly assigned at the start of the round, each group member gets a payoff a payoff of 50 EF.
Example 1: Suppose you are assigned p = 70, Purple is the color chosen by the vote, and the color of the Jar that is randomly assigned to your group is Purple.
Since you’re assigned p = 70, your payoff from Part A is: 100 – 70 = 30EF.
Since the color of the Jar assigned to your group is the same as the color chosen by your group in the vote, your payoff from Part B is: 50EF.
Thus, your total payoff from the voting task is: 80EF
Example 2: Suppose you are assigned p = 70, Brown is the color chosen by the vote, and the color of the Jar that is randomly assigned to your group is Purple.
You earn 70 EF from the voting task.
Since you’re assigned p = 70, your payoff from Part A is: 70 EF.
Since the color of the Jar assigned to your group is NOT the same as the color chosen by your group in the vote, your payoff from Part B is: 0EF.
Thus, your total payoff from the voting task is: 70EF.
Buying Information
Remember that none of the group members know the color of the Jar that has been randomly assigned to a group prior to voting on a color. Each group member has an option to buy multiple units of
information.
If a group member purchases information, he/she will observe a Report, which is either Brown or Purple. The probability that the color of this Report is the same as the color of the Jar depends on how many units of information the group member purchases.
Each group member can buy any number of units between 0 and 9 (in increments of one unit). If a group member buys a single unit of information, their Report is correct 55% of the time. If a group member purchases two units of information, their Report is correct 60% of the time. Each additional unit of information that a group member purchases increases the probability that their report is correct by 5
You can think of this process as the computer starts with a box with 50 Brown and 50 Purple balls. Each unit of information a group member purchases the computer adds 5 balls with the color of the Jar randomly assigned and removes 5 balls of the other color. The computer then mixes the balls and selects one randomly. The color of this selected ball is the color in the Report. So, for example, if a group member buys four units of information, the box from which the computer randomly selects a ball contains 70 balls with the color of the Jar which is randomly assigned and 30 balls of the other color. The cost of units of information is detailed in the table below.
If a group member chooses not to buy any units of information, they do not get a Report.
Example: Suppose you choose to buy 5 units of information and your Report is Brown.The cost of the 5 units of information is 13 EF,and there is a 75% chance the information is correct.
Connections
Only in communication treatments
At the start of each stage all group members are following each other on the message board. After each group member has decided how many units of information they wish to purchase, and viewed their Reports (when applicable), each group member decides who they would like to follow on the group’s message board.
Each group member can only see Posts made by group members they are following. Each group member is identified by the Subject ID assigned to them at the beginning of each stage. Remember that the Subject ID assigned to each group member remains the same within a stage.
Note that if you follow a particular group member, but they do not follow you, then they do not see your posts.
Post Choice
Only in communication treatments
After connection decisions have been made, each group member is shown:
- Group members they are
- Group members who are following
Each group member then chooses whether or not to make a Post.
Post Creation
Only in Full Communication treatment
Each group member who has opted to make a post determines the following contents of their post:
- p randomly assigned to the group: The group member can input a number between 0 EF and 100 EF. Their Post will state that the inputted number is the value of p assigned to them. Note that the number imputed does not have to be equal to their p. He/She can also opt not to input a number.
- Units of information the group member purchased: Each group member states the number of units of information they purchased. He/She can input any whole number between 0 and 9. Note that the number they state does not have to be equal to the actual number of units of information they purchased.
- The group member states the color of their Report, if they state they have purchased one or more units of Notice that the color they state does not have to equal the actual color of their Report.
Post Creation
Only in Truthful Communication treatment
If a group member chooses to share a Post will be populated with the following information from the information buying step:
- Units of information the group member purchased.
- The group member states the color of their Report, if the group member purchased one or more units of information.
The group member has the choice whether they want to disclose the value of p assigned to them.
Note: If a group member choose to share a post, he/she can’t alter the information about the number of units of information they purchased and the color of the report they received will be displayed on the group message board. However, they can choose whether they want to disclose the value of p.
Viewing posts on the message board
Only in communication treatments
Each group member will observe the Posts of those they are following, provided they decided to make a Post.
Example 1: Suppose your assigned Subject ID is C and you choose to follow Subjects B, D, and E, and not follow Subject A. Further suppose only Subject A and Subject B chose to create Posts. Since you follow Subject B, you will see their Post. Since you are not following Subject A, you will not see their Post.
Example 2: Suppose your assigned Subject ID is C, and Subjects A and E choose follow you, while Subjects B and D choose not to follow you. Further suppose that you decide to make a Post. Subjects A and E will see your Post, while Subjects B and D will not see your Post.
Vote
Each group member casts a vote for either: Brown or Purple.
In all treatments
Each group cast their vote without knowing the votes of the other members of their group.
The computer sums up the number of votes for Brown and for Purple. The color which receives three or more votes is the group’s decision.
Final Payoff
Each group member’s final payoff for the round is given by:
Final Payoff = Payoff from Voting – Total cost of buying information
Remember that the payoff of each group member in the round depends on the outcome of the vote, and the number of units of information they purchased.
Remember that there are two parts of the payoff from Voting:
Part A: Each group member gets p EF if the group votes for Brown, and 100 – p EF if the group votes for Purple. This payoff does not dependent on the color of the Jar, which is randomly assigned at the start of each round.
Part B: If the group’s decision matches the color of the Jar that was randomly assigned at the start of the round, each group member get a payoff a payoff of 50 EF.
Example: Suppose you are assigned p = 70, the group’s decision is Purple, and the color of the randomly assigned jar is Purple. Further suppose that you purchased 5 units of information and got a Brown Report.
Your final payoff for the round is 67 EF. You get 30EF from the group’s decision being Purple (Part A) plus you 50 EF since the group’s decision matched the color of the randomly selected jar (Part B) minus 13 EF for buying 5 units of information.
Appendix B: Additional Tables
Table A1. Quality of group decision making
Table A2. Average units of information purchased
Table A3. Total units of information purchased
Table A4. Total Number of Group Members Purchasing Information
Table A5. Number of Connections
Figure A1. Proportion of group members sharing a post
Table A6. Proportion of group members sharing a post
Table A7. Total units of information
Table A8. Units of information (mean)
Table A9. Add caption
Table A10. Simulation
Table A11. Composition of information shared
Appendix C: Proof
Theorem 1. In the model with heterogeneous preferences, if , there is an equilibrium with information acquisition, and it is unique within the class of equilibria with information acquisition. The equilibrium mapping is
(3)
Proof. For , it is easy to show that a best-responding voter will put probability zero on the set of actions
. If all voters put
and make an informed decision, there is a positive probability that they are pivotal given a state. But then, if
, a best-responding voter will put probability zero on the actions (0, A, B) and (0, B, A). It is easy to check that an information acquisition equilibrium mapping must order the action:
- (0,B,B) for
- (0,A,A) for
. If
. The probability that a voter is decisive in state
would be larger than the probability the voter is decisive in state
. But then if the voter is indifferent between acquiring information or playing (0, A, A) if
, then the voter should prefer to acquire information if
. Since
, the probability of being decisive in an equilibrium with information acquisition is the same in both states. Denoting this probability
we get that for
, the information quality chosen in equilibrium
must maximize.
\noindent Condition for would always vote for A
Finding for an interior solution
(4)
\noindent For an interior solution for
(5)
Using condition to solve for
(6)
Probability of being pivotal
(7)
References
Battaglini, M., R. B. Morton, and T. R. Palfrey (2010). The swing voter’s curse in the laboratory. Review of Economic Studies 77(1), 61–89.
Bhattacharya, S., J. Duffy, and S. Kim (2017). Voting with endogenous information acquisition: Experimental evidence. Games and Economic Behavior 102, 316–338.
Boxell, L., M. Gentzkow, and J. M. Shapiro (2018). A note on internet use and the 2016 US presidential election outcome. PloS One 13(7), e0199571.
Elbittar, A., A. Gomberg, C. Martinelli, and T. R. Palfrey (2016). Ignorance and bias in collective decisions. Journal of Economic Behavior & Organization.
Feddersen, T. J. and W. Pesendorfer (1996). The swing voter’s curse. American Economic Review, 408–424.
Fischbacher, U. (2007). z-tree: Zurich toolbox for ready-made economic experiments. Experimental economics 10(2), 171–178.
Garz, M., J. Sörensen, and D. F. Stone (2020). Partisan selective engagement: Evidence from Facebook. Journal of Economic Behavior & Organization 177, 91–108.
Goeree, J. K. and L. Yariv (2011). An experimental study of collective deliberation. Econometrica 79(3), 893–921.
Grosser, J. and M. Seebauer (2016). The curse of uninformed voting: An experimental study. Games and Economic Behavior 97, 205–226.
Guarnaschelli, S., R. D. McKelvey, and T. R. Palfrey (2000). An experimental study of jury decision rules. American Political Science Review 94(2), 407–423.
Jin, G. Z., M. Luca, and D. Martin (2015). Is no news (perceived as) bad news? an experimental investigation of information disclosure. Technical report, National Bureau of Economic Research.
Le Quement, M. T. and I. Marcin (2019). Communication and voting in heterogeneous committees: An experimental study. Journal of Economic Behavior & Organization.
Martinelli, C. (2006). Would rational voters acquire costly information? Journal of Economic Theory 129(1), 225–251.
Pogorelskiy, K. and M. Shum (2019). News we like to share: How news sharing on social networks influences voting outcomes. Available at SSRN 2972231.
Smith, V. L. (1982). Microeconomic systems as an experimental science. The American Economic Review 72(5), 923–955.