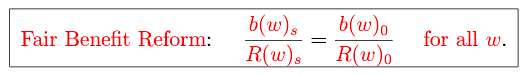Social Security and the Increasing Longevity Gap

Caliendo, Frank; Sheshinski, Eytan

1. Introduction

According to estimates in the 2017 Social Security Trustees Report, the Trust Fund will be fully depleted by 2034, at which time Social Security revenues will only cover approximately threequarters of promised benefits. The fiscal insolvency of Social Security is driven in part by growth in the overall life expectancy of the population, which strains the federal budget as retirees on average collect benefits over a longer retirement period.¹ To restore fiscal balance to the Social Security system, policy makers must increase taxes or reduce outlays or both.²

In thinking about the design of potential reforms, one fact really stands out: the increase in life expectancy has not occurred equally among the rich and poor. The largest gains have occurred among the wealthy. For instance, the male life expectancy gap between the richest and poorest quintiles in the US is 5.1 years for the 1930 birth cohort and is 12.7 years for the 1960 birth cohort (Auerbach et al. (2017)).³ In light of this fact, we develop simple reform options that address differential increases in longevity and restore solvency to the Social Security system.

Specifically, this paper does four things. First, we develop a simple way to summarize the degree of progressivity within a Social Security system. Our measure of progressivity is the variance of the implicit transfer share. The process for computing this summary statistic is as follows. We begin by computing the implicit transfer received by each wage type in the wage distribution, which is the difference between the benefits collected by retirees of a given wage type and the taxes paid by that wage type. We then express the implicit transfer for each wage type as a share of the total taxes paid by that type, and we refer to this as the implicit transfer share. Finally, we compute the variance of the implicit transfer share across all wage types in the wage distribution. The result is a summary statistic that characterizes the progressivity of a Social Security system.⁴

Second, using our measure of progressivity, we show that growth in the gap in life expectancy between the rich and poor (as in Auerbach et al. (2017)) erases three-quarters of the progressivity of the US Social Security system. Whether the government chooses to restore fiscal solvency with an across-the-board tax increase or an across-the-board proportional benefit cut, the end result is the same: the variance of the implicit transfer share for the 1960 birth cohort is just one-quarter of its value for the 1930 birth cohort. In other words, three decades of growth in the life expectancy gap unwinds most of the progressivity of the Social Security system.

Third, we develop two simple reform options that make the system fiscally sound without disrupting its progressivity. We refer to these as “fair” reforms for convenience and simplicity.⁵ The first reform involves increasing the Social Security tax rate the most among wage categories that experience the largest gains in life expectancy. To be precise, policy makers could adjust the Social Security tax rate across the wage distribution to preserve the variance of the implicit transfer share and hence preserve the progressivity of Social Security. The second reform follows the same principle by cutting benefits the most among wage categories that experience the largest gains in life expectancy. This, too, could be done in a way that restores fiscal solvency while keeping the variance of the implicit transfer share constant across cohorts.

Fourth, we estimate the welfare effects associated with fair reforms relative to across-theboard reforms. We augment the textbook life-cycle model with survival risk (Bütler (2001), Yaari (1965)) to include heterogeneity in wage earnings, heterogeneity in survival probabilities, and a Social Security program. We assume an individual’s wage earning type is random and welfare is measured by ex ante expected utility. In our baseline model, individuals would be willing to give up 0.8% of their total lifetime consumption to live in a world with fair tax reform rather than a world with an across-the-board tax increase. Similarly, individuals would give up 3.0% of their lifetime consumption to live in a world with fair benefit reform rather than a world with an across-the-board proportional benefit cut. The precise magnitude of these welfare gains depends on the degree of risk aversion of the individual, and these gains tend to vanish as we approach risk neutrality.

Finally, two important qualifications are in order. First, we do not tackle the (philosophical) question of what the policy goal should be. Likewise, we do not claim that our reforms satisfy a first-best strategy, nor do we provide a comprehensive welfare ranking of the many potential Social Security reforms that could be pursued. Instead, we show what would be required if the goal is to preserve the progressivity of the implied transfers. Second, our assumption that wage heterogeneity is the result of underlying uncertainty is non-trivial. A different view is that wage heterogeneity is entirely or in part the result of heterogeneity in effort. If so, then the role for insurance is less clear than when low wages represent unlucky draws from a probability distribution. While we do not weigh into this complex debate, we emphasize that the positive welfare effects of our simple reforms rely heavily on our assumption that wage earnings are uncertain.

1.1. Literature Review

The Social Security Administration (SSA) regularly evaluates different policy proposals that might restore solvency to the Social Security system. As of February 28, 2017, the Office of the Chief Actuary reported the fiscal impact of 60 different proposals for reforming Social Security in their analysis entitled Summary of Provisions that would Change the Social Security Program.⁶

The reform options that we study are similar to some of the proposals evaluated by the SSA. For instance, Proposal B3.1 calls for benefit reductions across the income distribution that (coincidentally) align fairly closely with the benefit reform option that we consider. In fact, many of the proposals that they consider involve targeted cuts to the benefits of those in the upper portion of the income distribution. Proposal B2.1 is perhaps closest to the benefit reform that we study because it involves automatic reductions in future Social Security benefits in response to growth in life expectancy. However, that proposal calls for across-the-board reductions in benefits in response to aggregate increases in life expectancy, while we study a reform option that links benefit reductions to life expectancy gains by wage category.

Broadly speaking, many of the proposals evaluated in recent years by the Office of the Chief Actuary focus on protecting the financial position of low-income households.⁷ While across-the-board tax increases and benefit cuts are useful guides for thinking about the overall magnitude of the fiscal adjustments that are needed to restore solvency, policy makers are currently considering a wide range of different reform structures. The options developed in our paper show what is required if policy makers wish to make the system fiscally sound without disrupting its progressivity.

The academic literature on Social Security is too extensive to properly summarize here. Instead, we briefly highlight a few strands of literature that are relevant to our paper.

In the US and in many other countries around the world, the Social Security benefit-earning rule is progressive in the sense that benefits as a fraction of pre-retirement earnings are larger for the poor than for the rich. From the perspective of economic theory, one may rationalize this feature of Social Security as insurance against bad earnings realizations (e.g., see Cremer, De Donder, Maldonado, and Pestieau (2008) and Cremer and Pestieau (2011)). However, other researchers challenge this rationale for Social Security. For instance, Bagchi (2015) argues that distortions to labor supply decisions unwind most of the welfare gains from Social Security’s insurance role, and Bagchi (2017) argues that the optimal benefit-earning rule is linear rather than progressive because high mortality risk among the poor would lead to heavy discounting of the consumption of the elderly poor in the calculation of utilitarian social welfare. Alternatively, in the model that we develop, maintaining the progressivity of Social Security is welfare improving relative to reforms that do not preserve the progressivity.

In addition to income insurance, Social Security pays benefits as a life annuity, which allows individuals to hedge their longevity risk. This feature is especially helpful in the absence of private annuity markets but can make adverse selection problems worse in their presence (Hosseini (2015)). Also, Social Security crowds out equilibrium bequest income, which can unwind the welfare gains from mandatory annuitization even in the absence of a bequest motive (Caliendo, Guo, and Hosseini (2014)). However, Social Security’s life annuity feature confers large welfare gains in our model because we conduct a micro-level welfare analysis with closed annuity markets. Haan, Kemptner, and Lüthen (2017) calculate how the increasing longevity gap affects the distribution of Social Security wealth in Germany, which is similar in spirit to our calculations of the implicit transfer share by income group and by cohort in the US. In addition to differences in the German and US Social Security systems, the papers diverge in that Haan, Kemptner, and Lüthen focus on surviving spouse issues while we study potential reform options.

Holzmann, Alonso-Garcia, Labit-Hardy, and Villegas (2017) propose reform options for nonfinancial defined contribution (NDC) pension systems. Their options are designed to eliminate the regressivity in NDC systems imposed by pooled annuities under differential mortality. Although we study a pay-as-you-go Social Security system rather than an NDC system, the principle behind their reform options is essentially the same as the reforms that we study. They suggest that annuities in NDC systems should be individualized rather than based on average life expectancies, or that the contribution rate in the NDC system should be individualized. In addition, the implicit transfer shares that we compute for Social Security are conceptually similar to the subsidy rates that they compute for NDC systems.⁸ Our paper differs from theirs because they focus on NDC systems while we measure the degree of progressivity in Social Security and we study reforms that maintain the system’s progressivity in the face of a growing life expectancy gap. Finally, our paper is motivated by the well-known observation that differential mortality risk between the rich and poor can partially undo the progressivity of the benefit-earning rule (e.g., Coronado, Fullerton, and Glass (2011)). We focus on the implications of growth in the life expectancy gap, and we study reform options that are designed specifically to address this phenomenon.

2. The Facts

In this section we develop a simple way to summarize the degree of progressivity in the current Social Security system. We then use this method to analyze the impact of the growing gap in life expectancy on the progressivity of Social Security.

2.1 Our Measure of Progressivity

In order to introduce our measure of progressivity, we need to build up some notation and assumptions. Age is continuous and is indexed by $t$ . At each moment in time an infinitely divisible cohort of unit mass is born. Individuals are born at $t = 0$ and die no later than $t = T$ . At birth, individuals realize their earning type, $w$ , which is a random variable with p.d.f. $g(w)$ and support normalized to the unit interval $[0, 1]$ . Individuals earn wages at rate w until they retire at age $t_R$ , after which they collect a constant Social Security benefit $b(w)$ in the form of a life annuity. Wage income is taxed at the Social Security tax rate $\tau$ . For simplicity, we abstract from population growth and wage growth.

The probability of surviving to age $t$ from the perspective of age 0 is $S(t \mid w)$ , where $S(0 \mid w)=1$ and $S(T \mid w)=0$ for all $w$ . For consistency with the data, we assume the rich have a higher probability of survival to each age than do the poor, $\partial S(t \mid w) / \partial w>0$ for all $t$ .

Hence, individuals in our model face two types of risk. First, they face ex ante risk (before birth) about their wage type. This risk is cleared up as soon as they are born, and after birth there are no idiosyncratic shocks to wages over the life cycle. The purpose of this risk in our model is to create heterogeneity in wage earnings. Second, individuals face ongoing risk over the life cycle about the timing of death, and the distribution of this risk depends on the wage type. However, there is no aggregate risk in the model since the distributions of both risks are known and the population mass is infinitely divisible and therefore covers the full support of realizations (law of large numbers).

For modeling purposes, the aggregate Social Security budget is balanced at each moment (pay-as-you-go). In other words, the tax rate $\tau$ must satisfy the government’s budget constraint for a given benefit-earning rule $b(w)$ so that aggregate taxes and benefits are equal

$\tau \int_0^1 \int_0^{t_R} g(w) S(t \mid w) w d t d w=\int_0^1 \int_{t_R}^T g(w) S(t \mid w) b(w) d t d w.$

Notice that the budget doesn’t need to balance separately for each wage type. Instead, Social Security pools the contributions of all workers to pay an annuity to retirees, and there is cross subsidization across wage groups because benefits depend on wages and because survival probabilities depend on wages. To measure redistribution, note that each earning type receives an implicit transfer $\Delta(w)$ defined as the difference between what that type receives in benefits and what they pay in taxes⁹

$\tau \int_0^{t_R} S(t \mid w) w d t+\Delta(w)=\int_{t_R}^T S(t \mid w) b(w) d t,$

where the average transfer must be zero to satisfy the aggregate budget constraint,

$\int_0^1 g(w) \Delta(w) d w=0.$

For convenience, let $\delta(w)$ be the implicit transfer share, which is the implicit transfer received by type $w$ as a share of total taxes paid by type $w$ ,

$\delta(w) \equiv \frac{\Delta(w)}{\tau \int_0^{t_R} S(t \mid w) w d t}.$

While there are a variety of ways to define the degree of progressivity of a Social Security system, we conveniently define the degree of progressivity as the variance of the implicit transfer share

$\operatorname{var}(\delta(w))=\int_0^1 g(w)[\delta(w)-\mathbb{E}(\delta(w))]^2 d w.$

Our measure of progressivity has the advantage of summarizing the progressivity of the current system with a single statistic. Notice that the special case of a (Bismarckian) system devoid of any redistribution would have $\Delta(w)=0$ for all $w$ and $\operatorname{var}(\delta(w))=0$ follows mathematically. For all other systems with at least some redistribution, $\operatorname{var}(\delta(w))>0$ .

We should mention one caveat with our measure of progressivity. A regressive system would also lead to positive variance of the implicit transfer share. Therefore, our measure of ìprogressivityîactually picks up any type of redistribution, but this distinction is immaterial for our paper because all of our numerical simulations correspond to the actual (progressive) distribution of the implicit transfer share in the US.

2.2. The Effect of a Growing Life Expectancy Gap on the Degree of Progressivity

To assess how the growing gap in life expectancy across the rich and poor affects the progressivity of Social Security, we need to calibrate three functions: $b(w)$ , $g(w)$ , and $S(t \mid w)$ .

The Social Security benefit-earning rule b(w) is a piecewise linear function of an individual’s 1 wage. Following Alonso-Ortiz (2014) and others, we assume the Social Security bend points are the following constant multiples of the economy-wide average wage, 0.2, 1.24, and 2.47. Social Security replaces 90% of the individual’s wages up to the first bend point, 32% of wages between the first and second bend points, 15% of wages between the second and third bend points, and 0% of wages beyond the third bend point.

In order to develop numerical examples, we assume that wages follow a beta distribution with density as in Slavov, Gorry, Gorry, and Caliendo (2017)

$g(w)=\frac{w^{\gamma-1}(1-w)^{\beta-1}}{\int_0^1 w^{\gamma-1}(1-w)^{\beta-1} d w}, \text { for } w \in[0,1].$

To abstract from the portion of the wage distribution above the third bend point, they calibrate $g(w)$ so that the top wage earner with $w = 1$ earns 2.47 times that of the average earner.¹⁰ Since $\mathbb{E}(w)=\gamma /(\gamma+\beta)$ , they set $\gamma=\beta / 1.47$ to ensure that $\mathbb{E}(w)=1 / 2.47$ for any choice of $\beta$ . Then, to approximate the dispersion of wages they choose $\beta=1.8$ , which delivers the following Gini coefficient

$\text { Gini }=\frac{1}{2 \mathbb{E}(w)} \int_0^1 \int_0^1 g(x) g(y)|x-y| d x d y=0.3463.$

Based on estimates in Leonesio and Del Bene (2011), we assume that a Gini coefficient of 0.3463 is fairly close to the Gini coefficient in 1980 when the 1930 cohort from Auerbach et al. (2017) turned 50.¹¹ Of course, wages have become more dispersed in the last few decades, but our focus is on the implications of a growing gap in life expectancy so we intentionally hold $g(w)$ fixed throughout the analysis. While our calibration of the wage distribution is obviously an approximation of the true distribution, we emphasize that the reform options that we develop below do not rely on the particular wage distribution that we assume. We make assumptions about the wage distribution in order to understand the potential welfare effects of the reforms that we study.

Auerbach et al. provide data on life expectancies at age 50 by income quintile for the 1930 and 1960 birth cohorts. We calibrate the $S(t \mid w)$ function using their life expectancy estimates for the 1930 cohort as the baseline, and then we examine how the 1960 life expectancy estimates change the progressivity of Social Security. Note that additional years of life expectancy conditional on surviving to some age $t^{\prime}$ for type $w$ is

$\mathcal{L}\left(t^{\prime}, w\right) \equiv \frac{1}{S\left(t^{\prime} \mid w\right)} \int_{t^{\prime}}^T\left(-\frac{\partial S(t \mid w)}{\partial t}\right) t d t-t^{\prime}=\frac{1}{S\left(t^{\prime} \mid w\right)} \int_{t^{\prime}}^T S(t \mid w) d t.$

We assume work starts at age 18 and lasts until retirement age 67, with death occurring no later than age 100.¹² We normalize the economic lifespan onto the unit interval so that age 18 corresponds to model age 0 and age 100 corresponds to model age $T = 1$ . Likewise, age 50 corresponds to model age $t^{\prime}=(50-18) /(100-18)=0.390$ . The life expectancy of the 1930 cohort at age 50 is 31.7 years for the richest group (or 31.7=82 = 0.387 in model units) and 26.6 years for the poorest group (or 26.6=82 = 0.324 in model units). We assume survival functions take the form

$S(t \mid w)=1-t^{x(w)},$

where the parameter $x(w)$ is specific to each wage type. We choose the survival functions for the top and bottom of our earnings distribution in order to replicate the life expectancy gap documented by Auerbach et al. In other words, $x(1)$ is calibrated such that $\mathcal{L}\left(t^{\prime} \mid 1\right)=31.7 / 82$ and $x(0)$ is calibrated such that $\mathcal{L}\left(t^{\prime} \mid 0\right)=26.6 / 82$ , while all other x values are a convex combination

$x(w)=x(1) w+x(0)(1-w).$

Doing so gives $x(1) = 2.953$ and $x(0) = 1.433$ . Our approach is an approximation of the mapping from the wage distribution to life expectancy.

Using the benefit-earning rule and wage density given above, we find that the balanced-budget tax rate is 11.2% if we use the survival probabilities for the 1930 birth cohort. More to the point, the variance of the implicit transfer share is $\operatorname{var}(\delta(w))=0.0867$ .¹³

Next, we compare to the 1960 birth cohort. We hold the benefit-earning rule and the wage density fixed and move to the survival probabilities associated with the 1960 cohort so that we can examine the implications of the growing gap in life expectancy on the Social Security budget. The life expectancy of the 1960 cohort at age 50 is 38.8 years for the richest group (or 38.8=82 = 0.473 in model units) and 26.1 years for the poorest group (or 26.1=82 = 0.318 in model units). Following the same procedure as above gives $x(1) = 6.253$ and $x(0) = 1.301$ . This change in longevity makes the system insolvent under the current tax and benefit schedule. For across-the-board tax reform, we find that the balanced-budget tax rate must rise to 14.5%, and the variance of the implicit transfer share shrinks to $\operatorname{var}(\delta(w))=0.0246$ .¹⁴ In other words, a pay-as-you-go system would lose nearly three-quarters of its progressivity as the life expectancy gap widens.

Of course, fiscal solvency could be achieved through a proportional benefit cut as well. Rather than increase the tax rate from 11.2% to 14.5%, our model suggests that reducing the entire benefit schedule to 77.47% of its current level would also restore solvency.¹⁵ Doing this also causes the variance of the implicit transfer share to shrink to $\operatorname{var}(\delta(w))=0.0246$ , the same as for the case of a tax increase, and again the pay-as-you-go system loses nearly three-quarters of its progressivity as the life expectancy gap widens. Across-the-board tax increases and across-the-board proportional benefit cuts have the same destructive effect on the progressivity of the Social Security system.

Figure 1 plots the data behind these results in order to visualize the magnitude of the implicit transfer shares as well as the loss in progressivity from a widening life expectancy gap. For the 1930 cohort, the shares are calculated using current Social Security taxes and benefits. For the 1960 cohort, the shares are calculated under the assumption that policy makers have pursued either an across-the-board tax increase or an across-the-board proportional benefit cut (the shares are the same irrespective of whether it is the former or the latter reform). For example, the largest transfer recipients (individuals at the first bend point) in the 1930 cohort receive benefits that are 89% larger than the taxes that they pay, while benefits are 53% larger than taxes paid for the same recipients in the 1960 cohort. Almost all individuals above the mean wage (approximately $w = 0.4$ ) in the 1960 cohort receive a larger transfer share than their counterparts in the 1930 cohort.

3. Two Reforms

In this section we develop two reforms to Social Security. One is a tax increase and the other is a benefit cut. But rather than across-the-board reforms that would ignore the growing gap in life expectancy, both of the reforms that we develop are “fair” in the sense that they maintain the progressivity of the Social Security system. While growth in life expectancies creates a major fiscal challenge for policy makers, we explore targeted reforms that not only close the fiscal gap but do so in a way that recognizes that life expectancy gains have not occurred evenly across the income distribution.

Before presenting the reform options, it is helpful to note that the implicit transfer share can be rewritten for convenience as

$\delta(w) \equiv \frac{\Delta(w)}{\tau \int_0^{t_R} S(t \mid w) w d t}=\frac{\int_{t_R}^T S(t \mid w) b(w) d t-\tau \int_0^{t_R} S(t \mid w) w d t}{\tau \int_0^{t_R} S(t \mid w) w d t}=\frac{b(w)}{\tau w R(w)}-1,$

where $R(w)$ is the ratio of workers to retirees among type- $w$ individual

$R(w)=\frac{\int_0^{t_R} S(t \mid w) d t}{\int_{t_R}^T S(t \mid w) d t}.$

With this notation in mind, we discuss two reform options.

3.1 Option #1: Fair Tax Reform

This potential reform maintains the progressivity of Social Security through a simple tax adjustment that responds to asymmetries in life expectancy growth across the wage distribution. The basic idea is that wage types who experience the greatest gains in life expectancy would face the greatest increase in their contribution rate.

Specifically, notice that to hold the variance of the implicit transfer share $\operatorname{var}(\delta(w))$ constant over time, it is enough to hold the transfer shares themselves $(w)$ constant over time for each $w$ . One way to do this is to hold constant over time the product $R(w)$ within each wage type while leaving benefits $b(w)$ intact. That is, policy makers could create a wage-dependent (progressive) tax $(w)$ that adjusts according to the following rule for some future calendar date $s > 0$
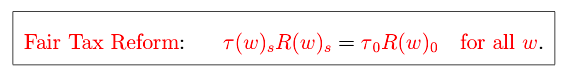
If we establish a base calendar year $(s = 0)$ , then policy makers could maintain the progressivity of Social Security that exists in that base year by charging a progressive tax that evolves over time as the ratio of workers to retirees evolves within each wage type. Notice that any wage type that experiences a reduction in the ratio of workers to retirees would need to contribute more to the system, and those wage types with the greatest longevity gains (the largest reduction in the ratio of workers to retirees) would face the largest increases in their contributions because they are responsible for placing the most strain on the Social Security budget. Figure 2 plots the fair tax reform function relative to across-the-board tax reform.

3.2. Option #2: Fair Benefit Reform

Another way to maintain the variance of the implicit transfer share (and therefore preserve the progressivity of Social Security) is to reform benefits in a way that responds to asymmetries in life expectancy growth across the wage distribution. To do this, we can hold benefits constant over time relative to the worker-to-retiree ratio, $b(w)/R(w)$ , within each wage type. In other words, to hold $\operatorname{var}(\delta(w))$ constant over time it is enough to hold $b(w)/R(w)$ constant over time within each wage type (holding the tax rate constant). To do so would require a progressive benefit cut according to the following rule for some future date $s > 0$

Like the fair tax reform option, this too brings fiscal balance to the Social Security system while preserving its progressivity. Figure 3 plots the fair benefit reform rule together with the across-the-board reform. Across-the-board reform keeps all of the bend points the same but reduces the slopes of the three segments from their current values of 90%, 32% and 15% down to 70%, 25%, and 12% (each new slope would be 77.47% of the current slope). But we showed previously that doing this would erase three-quarters of the progressivity of Social Security. The fair benefit reform option would also involve keeping the location of the bend points intact, but the slopes of the segments would change from their current values of 90%, 32% and 15% down to 86%, 21%, and 9%.¹⁶

3.3. Discussion

To summarize, the reform options that we study have three important features. First, as the overall longevity of the population increases, the Social Security system would automatically adapt to maintain its fiscal solvency. Second, asymmetric changes in longevity across income classes (such as the recent widening of the gap in life expectancy across the wage distribution) would be accounted for in a way that maintains the degree of progressivity inherent in the base year. Third, the required adjustments to either taxes or benefits are very simple to make; policy makers would only need to know the ratio of workers to retirees by wage category in order to make the adjustments.

While we have studied tax reform and benefit reform separately, one could design a hybrid reform option. Policy makers could pursue a mixture of tax and benefit reforms, and this could be done in a way that maintains progressivity. For instance, a small, uniform tax increase could be coupled with a targeted benefit cut that is designed to preserve the variance of the implicit transfer share. Moreover, it may be possible to preserve the variance of the implicit transfer share by adjusting the normal retirement age to be wage specific. We have presented only two of a variety of possible reforms.

4. Welfare Analysis

Our purpose here is to estimate the potential welfare effects associated with fair tax and benefit reforms relative to across-the-board reforms. We use a standard, Yaari-style model that has been augmented to include heterogeneity in wages, heterogeneity in survival risk, and a Social Security program.

Individuals consume and save rationally in the face of longevity risk and take into consideration Social Security taxes and benefits. An individual’s consumption is $c(t)$ and utility from consumption is $u(c(t))$ , where $u^{\prime}>0$ and $u^{\prime \prime}<0$ . Future utility is discounted at rate $p$ . Annuity markets are closed, and for simplicity all saving is done in a risk-free account, $k(t)$ , with interest rate $r$ .

At $t = 0$ individuals learn their wage type $w$ , and they take as given $\tau(w)$ , $b(w)$ , and choose $(c(t), k(t))_{t \in[0, T]}$ according to

$\max : U=\int_0^T e^{-\rho t} S(t \mid w) u(c(t)) d t,$

subject to

$\begin{gathered} \dot{k}(t)=r k(t)+(1-\tau(w)) w-c(t), \text { for } t \in\left[0, t_R\right] \\ \dot{k}(t)=r k(t)+b(w)-c(t), \text { for } t \in\left[t_R, T\right] \\ k(0)=0, k(T)=0 . \end{gathered}$

We denote the solution consumption path $c^*(t \mid w)$ . For CRRA utility $u(c)=c^{1-\sigma} /(1-\sigma)$ ,

$c^*(t \mid w)=\frac{\int_0^{t_R} e^{-r t}(1-\tau(w)) w d t+\int_{t_R}^T e^{-r t} b(w) d t}{\int_0^T S(t \mid w)^{1 / \sigma} e^{-r t+(r-\rho) t / \sigma} d t} S(t \mid w)^{1 / \sigma} e^{(r-\rho) t / \sigma}.$

Ex ante welfare is defined as¹⁷

$\mathbb{E}(U)=\int_0^1 \int_0^T g(w) e^{-\rho t} S(t \mid w) u\left(c^*(t \mid w)\right) d t d w.$

Define $c_{A B}^*(t \mid w)$ as the optimal consumption rule in a world where across-the-board reforms are pursued immediately (at $t = 0$ ), and $c_F^*(t \mid w)$ as the optimal consumption rule in a world where fair reforms are pursued immediately.¹⁸ The compensating variation, $CV$ , is defined as the percentage of lifetime consumption that individuals are willing to give up to live in a world with fair reform

$\int_0^1 \int_0^T g(w) e^{-\rho t} S(t \mid w) u\left(c_F^*(t \mid w)(1-C V)\right) d t d w=\int_0^1 \int_0^T g(w) e^{-\rho t} S(t \mid w) u\left(c_{A B}^*(t \mid w)\right) d t d w.$

The idea here is that reform is going to take place one way or another in our model, and we calculate the welfare gains associated with fair reform relative to across-the-board reform. Unless we say otherwise, we use $\sigma=1.5$ in the calculations below. Larger values of $\sigma$ will enhance the welfare gains from fair reform, while smaller values will reduce the welfare gains. We begin with the assumption $r=\rho=0$ , but we will report sensitivity analysis on this assumption.

We emphasize that our welfare analysis is simplified in at least three ways. First, our ex ante welfare measure is a steady-state measure that does not take into account the effects on transition generations. Such generations would be surprised by an announcement at any particular date and their lifetime well-being would be different than those born under the new system. Ignoring transition generations would tend to overstate the welfare gains from fair tax reform. For example, the welfare of workers who are close to retirement does not depend very much on whether the government pursues a fair tax reform or an across-the-board tax reform since these workers are almost done paying taxes anyway. Second, while our ex ante “behind the veil” welfare measure is standard, we could have used other welfare weights across the income distribution. For instance, we could put more weight on individuals in the low end of the distribution than is implied by the probability density function, and doing so could increase the welfare gains associated with the fair reforms that we study. Moreover, an improvement in our ex ante welfare measure does not imply a Pareto improvement in the sense that the individual is ex post better off for any wage realization. Third, while our analysis captures the standard connection between risk aversion and willingness to insure risk, the welfare effects generated by our model are simple approximations that do not capture the effects that different reform options might have on labor supply, capital formation, and factor prices.

4.1. Welfare Gains from Fair Tax Reform

We first compute the welfare gains from fair tax reform. To do this, we calculate consumption in the across-the-board reform world $c_{A B}^*(t \mid w)$ by solving the individual’s optimization problem with a constant Social Security tax rate of 14.5% over the entire life cycle since this is the common tax rate that, according to the calculations in our model, would be required to balance the aggregate Social Security budget. Likewise, we calculate consumption in a separate world with fair tax reform $c_F^*(t \mid w)$ by solving the individual’s optimization problem with a wage-dependent Social Security tax as calculated in the previous section to maintain progressivity (i.e., to ensure the variance of the implicit transfer share is the same for the 1960 and 1930 birth cohorts). In both worlds, we use the survival probabilities associated with the 1960 cohort as well as the current Social Security benefit-earning rule. We find $CV$ = 0.8%.

This exercise tells us the fraction of lifetime consumption that an individual would agree to give up, ex ante, to be born into a world with fair tax reform rather than a world with across-the-board tax reform. Rational, forward-looking individuals in our model will give up 0.8% of their entire lifetime consumption expenditure. These large welfare gains are because fair reform acts as an insurance device for individuals facing ex ante uncertainty about their wage type.

The coefficient of relative risk aversion $\sigma$ plays a vital role in the welfare calculations. This parameter is unobservable and subjective, and the welfare results are sensitive to its value. While the value that we are using falls within the range of values commonly used in the related literature, small changes in this parameter can cause significant changes in the welfare results. For instance, if $\sigma = 2$ then the $CV$ = 1.5%, which is nearly twice the size of the welfare gain when $\sigma = 1.5$ . On the other hand, if $\sigma = 0.5$ then the $CV$ = 0.1% and hence the welfare gain from fair reform is small. The direction of these results is intuitive: individuals become virtually indifferent between across-the-board reform and fair reform as their risk aversion tends to zero.

The parameters $r$ and $\rho$ do not affect the welfare calculations at the level of precision that we are reporting. For instance, holding $\sigma$ at its baseline value of 1.5, we continue to obtain $CV$ = 0.8% for all three of the following parameterizations: $r = 3%$ and $\rho = 0$ ; $r = 0$ and $\rho = 3%$ ; and $r = \rho = 3%$

4.2. Welfare Gains from Fair Benefit Reform

Alternatively, we repeat a similar exercise but for the case of benefit reform. We calculate consumption in the across-the-board reform world $c_{A B}^*(t \mid w)$ by solving the individualís optimization problem when Social Security benefits for each wage type are 77.47% of their current level (to keep the program solvent). This is known at $t = 0$ to abstract from policy uncertainty. And we calculate consumption in a separate world with fair benefit reform $c_F^*(t \mid w)$ by solving the individual’s optimization problem where the reduction in benefits maintains the progressivity of Social Security as described previously in our paper. In both worlds, we use the survival probabilities associated with the 1960 cohort and we leave the Social Security tax rate at its original level. We compute the compensating variation associated with fair benefit reform, which tells us the fraction of lifetime consumption that an individual would give up, ex ante, to be born into a world with fair benefit reform rather than across-the-board benefit reform. We find $CV = 3.0%$ . This is an enormous welfare gain by any standard. Fair benefit reform, relative to across-the-board benefit reform, is a particularly valuable hedge against bad wage realizations.

As with the case of tax reform, the coefficient of relative risk aversion $\sigma$ plays an important role in the welfare calculations. Small changes in this parameter can have large welfare implications. For instance, if $\sigma = 2$ then the $CV = 5.8%$ , which is nearly twice the size of the welfare gain when $\sigma = 1.5$ . On the other hand, if $\sigma = 0.5$ then the $CV = 0.7%$ . Our basic point does not depend on the precise value of $\sigma$ that we use, but the magnitudes of the welfare effects certainly do.

The parameters $r$ and $\rho$ have a small effect on the welfare calculations. Holding $\sigma$ at its baseline value of 1.5 we obtain: $CV = 2.9%$ when $r = 3%$ and $\rho = 0$ ; $CV = 3.1%$ when $r = 0$ and $\rho = 3%$ ; and $CV = 3.1%$ when $r = \rho = 3%$ .

4.3. Discussion

The decision between targeted (fair) tax reform and targeted benefit reform is a difficult policy decision that is beyond our scope. A number of additional (unmodeled) factors would potentially be important to policy makers in such a consideration. For instance, we abstract from labor supply decisions and from other forms of taxation that affect the total tax burden facing households, including income and investments taxes. We also abstract from irrational behavior and instead assume individuals make optimal saving decisions; hence, we do not consider Social Securityís potential role in providing income protection for retirees who undersave. A deeper analysis of these issues may be important in the overall decision between a tax increase and a benefit cut. Our focus is to separately consider tax and benefit reforms, and to quantify the magnitude of the adjustments that would be needed to pursue distributionally-neutral reforms.

5. Conclusion

High earners in the US have experienced large gains in life expectancy while those at the bottom of the earnings distribution have experience little or no gain in life expectancy. Therefore, high earners (on average) are responsible for the bulk of the projected fiscal strain on the Social Security system. We develop a measure of the progressivity of the Social Security system, and we track the degree to which the progressivity of the system is eroded by growth in the life expectancy gap. We find that the erosion of progressivity is economically significant, and we study welfare-improving reforms that are designed to maintain the progressivity of the system in the face of a widening life expectancy gap.

References

Auerbach, Alan J., Kerwin K. Charles, Courtney C. Coile, William Gale, Dana Goldman, Ronald Lee, Charles M. Lucas, Peter R. Orszag, Louise M. Sheiner, Bryan Tysinger, David N. Weil, Justin Wolfers, Rebeca Wong (2017), How the Growing Gap in Life Expectancy May Affect Retirement Benefits and Reforms. National Bureau of Economic Research, Working Paper 23329.

Alonso-Ortiz, Jorge (2014), Social Security and Retirement across the OECD. Journal of Economic Dynamics and Control 47, 300-316.

Bagchi, Shantanu (2015), Labor Supply and the Optimality of Social Security. Journal of Economic Dynamics and Control 58, 167-185.

Bagchi, Shantanu (2016), Is the Social Security Crisis Really as Bad as we Think? Macroeconomic Dynamics 20, 737-776.

Bagchi, Shantanu (2017), Differential Mortality and the Progressivity of Social Security. Working Paper, Towson University.

Bütler, Monika (1999), Anticipation Effects of Looming Public-Pension Reforms. CarnegieRochester Conference Series on Public Policy 50(1), 119-159.

Bütler, Monika (2001), Neoclassical Life-Cycle Consumption: A Textbook Example. Economic Theory 17, 209-221.

Caliendo, Frank N., Aspen Gorry, and Sita Slavov (2015), The Cost of Uncertainty about the Timing Social Security Reform. Utah State University Working Paper.

Caliendo, Frank N., Nick L. Guo, and Roozbeh Hosseini (2014), Social Security is NOT a Substitute for Annuity Markets. Review of Economic Dynamics 17, 739-755.

Coronado, Julia Lynn, Don Fullerton, and Thomas Glass (2011), The Progressivity of Social Security. B.E. Journal of Economic Analysis & Policy 11(1), 1-45.

Cremer, Helmuth, Philippe De Donder, Dario Maldonado, and Pierre Pestieau (2008), Designing a Linear Pension Scheme with Forced Savings and Wage Heterogeneity. International Tax and Public Finance 15(5), 547-562.

Cremer, Helmuth and Pierre Pestieau (2011), Myopia, Redistribution and Pensions. European Economic Review 55(2), 165-175.

Gomes, Francisco J., Laurence J. Kotlikoff, and Luis M. Viceira (2007), The Excess Burden of Government Indecision. National Bureau of Economic Research, Working Paper 12859.

Haan, Peter, Daniel Kemptner, and Holger Lüthen (2017), The Increasing Longevity Gap by Lifetime Earnings and its Distributional Implications. DIW Berlin Working Paper.

Holzmann, Robert, Jennifer Alonso-Garcia, Heloise Labit-Hardy, and Andrés M. Villegas (2017), NDC Schemes and Heterogeneity in Longevity: Proposals for Redesign. ARC Centre of Excellence in Population Ageing Research, Working Paper 2017/18.

Hosseini, Roozbeh (2015), Adverse Selection in the Annuity Market and the Role for Social Security. Journal of Political Economy 123, 941-984.

Kitao, Sagiri (2017), Policy Uncertainty and Cost of Delaying Reform: The Case of Aging Japan. Review of Economic Dynamics, forthcoming.

Leonesio, Michael V. and Linda Del Bene (2011), The Distribution of Annual and Long-Run US Earnings, 1981-2004. Social Security Bulletin 71(1), 17-33.

Luttmer, Erzo F. P. and Andrew A. Samwick (2012), The Welfare Cost of Perceived Policy Uncertainty: Evidence from Social Security. Dartmouth College Working Paper.

Slavov, Sita, Devon Gorry, Aspen Gorry, and Frank N. Caliendo (2017), Social Security and Saving: An Update. Working Paper, George Mason University.

Yaari, Menachem (1965), Uncertain Lifetime, Life Insurance and the Theory of the Consumer. Review of Economic Studies 32(2), 137-150.

Social Security and the Increasing Longevity Gap

Executive Summary

Resources

Focuses

House/Senate Committees

1. Introduction

1.1. Literature Review

2. The Facts

2.1 Our Measure of Progressivity

2.2. The Effect of a Growing Life Expectancy Gap on the Degree of Progressivity

3. Two Reforms

3.1 Option #1: Fair Tax Reform

3.2. Option #2: Fair Benefit Reform

3.3. Discussion

4. Welfare Analysis

4.1. Welfare Gains from Fair Tax Reform

4.2. Welfare Gains from Fair Benefit Reform

4.3. Discussion

5. Conclusion

References

Executive Summary

Resources

Related Publications

Related Publications

Related News

Related Blogs

Focuses

House/Senate Committees

1. Introduction

1.1. Literature Review

2. The Facts

2.1 Our Measure of Progressivity

2.2. The Effect of a Growing Life Expectancy Gap on the Degree of Progressivity

3. Two Reforms

3.1 Option #1: Fair Tax Reform

3.2. Option #2: Fair Benefit Reform

3.3. Discussion

4. Welfare Analysis

4.1. Welfare Gains from Fair Tax Reform

4.2. Welfare Gains from Fair Benefit Reform

4.3. Discussion

5. Conclusion

References